题目内容
在△ABC中,角A,B,C所对的边为a,b,c,已知已知
=
,且∠C=
.
(1)求角A,B的大小;
(2)设函数f(x)=sin(2x+A)+cos(2x-
),求函数f(x)在[-
,
]上的值域.
| cosA |
| cosB |
| b |
| a |
| 2π |
| 3 |
(1)求角A,B的大小;
(2)设函数f(x)=sin(2x+A)+cos(2x-
| C |
| 2 |
| π |
| 8 |
| π |
| 4 |
考点:解三角形,正弦函数的定义域和值域
专题:计算题
分析:(1)利用正弦定理可把已知条件化简可得,sin2A=sin2B,从而可得A=B或A+B=
(舍去),进而可求∠C=
,A=B=
(2)由(1)可得,∠C=
,A=B=
代入函数中整理可得,f(x)=2sin(2x+
),由x∈[-
,
],可得-
≤2x+
≤
,结合正弦函数y=sinx在[-
,
]上单调递增,在[
,
]上单调递减可求函数f(x)的最小值为f(-
)=
,最大值为f(
)=2.
即函数f(x)在[-
,
]上的值域为[
,2].
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
(2)由(1)可得,∠C=
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 8 |
| π |
| 4 |
| π |
| 12 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 12 |
| ||||
| 2 |
| π |
| 2 |
即函数f(x)在[-
| π |
| 8 |
| π |
| 4 |
| ||||
| 2 |
解答:
解:(1)因为
=
,由正弦定理得
=
,即sin2A=sin2B(2分)
所以,A=B或A+B=
(舍去),∠C=
,则A=B=
(4分)
(2)f(x)=sin(2x+A)+cos(2x-
)
=sin(2x+
)+cos(2x-
)=sin(2x+
)+cos(2x+
-
)=2sin(2x+
)(8分)
因为x∈[-
,
],则-
≤2x+
≤
,
而正弦函数y=sinx在[-
,
]上单调递增,在[
,
]上单调递减.(11分)
所以,函数f(x)的最小值为f(-
)=
,最大值为f(
)=2.
即函数f(x)在[-
,
]上的值域为[
,2](14分)
| cosA |
| cosB |
| b |
| a |
| cosA |
| cosB |
| sinB |
| sinA |
所以,A=B或A+B=
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
(2)f(x)=sin(2x+A)+cos(2x-
| C |
| 2 |
=sin(2x+
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
因为x∈[-
| π |
| 8 |
| π |
| 4 |
| π |
| 12 |
| π |
| 6 |
| 2π |
| 3 |
而正弦函数y=sinx在[-
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
所以,函数f(x)的最小值为f(-
| π |
| 12 |
| ||||
| 2 |
| π |
| 2 |
即函数f(x)在[-
| π |
| 8 |
| π |
| 4 |
| ||||
| 2 |
点评:本题主要考查了正弦定理在解三角形中的应用,两角和与差的三角公式,正弦函数在闭区间上的函数的值域的求解,综合的知识较多,综合性较好.

练习册系列答案
相关题目
 如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.
如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.| A、504 | B、501 |
| C、500 | D、550 |
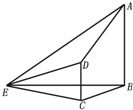 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.