题目内容
过点A(2,0)的直线把圆x2+y2≤1(区域)分成两部分(弓形),它们所包含的最大圆的直径之比是1:2,则此直线的斜率是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:先画出草图,判断两个内切圆的位置,根据直径比求出大圆圆心到直线的距离.后根据三角恒等变化求解即可
解答:
解:如图所示,过点O作OC⊥l交圆O与A,B两点
则|BC|和|AC|分别是两个弓形内切圆的直径
∴
=
或
=2
即
=2.
解得,|OC|=
设直线l的倾斜角为α,
则sin(π-α)=
=
,或sinα=
∴sinα=
,
∴tanα=±
=±
即此直线的斜率是±
故答案为±
则|BC|和|AC|分别是两个弓形内切圆的直径
∴
| |BC| |
| |AC| |
| 1 |
| 2 |
| |BC| |
| |AC| |
即
| 1+|OC| |
| 1-|OC| |
解得,|OC|=
| 1 |
| 3 |
设直线l的倾斜角为α,
则sin(π-α)=
| |OC| |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
∴sinα=
| 1 |
| 6 |
∴tanα=±
| sinα | ||
|
| ||
| 35 |
即此直线的斜率是±
| ||
| 35 |
故答案为±
| ||
| 35 |
点评:本题主要考查了直线与圆的位置关系,点到直线的距离公式,以及三角恒等变换等知识的综合应用,属于难题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
抛物线y2=2px(p>0)的焦点为F,已知点A,B为抛物线上的两个动点,且满足∠AFB=90°.过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则
的最大值为( )
|
| ||
|
|
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知椭圆的两个焦点和短轴的两个端点恰好为一个正方形的四个顶点,则该椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
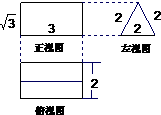 已知某个几何体的三视图如图所示,试根据图中所标出的尺寸(单位:cm),可得这个几何体的表面积是( )
已知某个几何体的三视图如图所示,试根据图中所标出的尺寸(单位:cm),可得这个几何体的表面积是( )A、18+
| ||
B、18+2
| ||
C、24+2
| ||
D、24+2
|
直线x+
y-2=0被圆(x-1)2+y2=1所截得的弦长为( )
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
