Question

抛物线y²=2px（p＞0）的焦点为F，已知点A，B为抛物线上的两个动点，且满足∠AFB=90°．过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则

| MN |

| AB |

的最大值为（　　）

• A、

  2

  2

• B、

  3

  2

• C、1
• D、

  3

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：设|AF|=a，|BF|=b，由抛物线定义，2|MN|=a+b．再由勾股定理可得|AB|²=a²+b²，进而根据基本不等式，求得|AB|的范围，即可得到答案．

解答： 解：设|AF|=a，|BF|=b，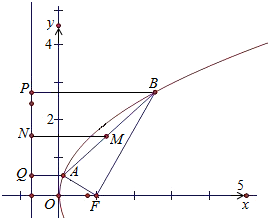
由抛物线定义，得AF|=|AQ|，|BF|=|BP|
在梯形ABPQ中，∴2|MN|=|AQ|+|BP|=a+b．
由勾股定理得，|AB|²=a²+b²配方得，
|AB|²=（a+b）²-2ab，
又ab≤(

a+b

2

)2，
∴（a+b）²-2ab≥（a+b）²-2(

a+b

2

)2，
得到|AB|≥

2

2

（a+b）．
∴

| MN |

| AB |

≤

1 2 (a+b)

2 2 (a+b)

=

2

2

，即

| MN |

| AB |

的最大值为

2

2

．
故选A．

点评：本题主要考查抛物线的应用和解三角形的应用，考查基本不等式，考查了计算能力、分析问题和解决问题的能力．