Question

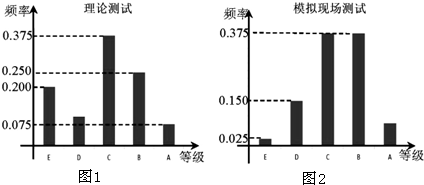
某校政教处为检查各班落实学校“学生素养五十条”的规定情况，从各班抽取了一批学生进行测试，全部学生参加了“理论部分（如图1）”和“模拟现场（如图2）”两项测试，成绩均分为A，B，C，D，E五个等级．某考场考生两项测试成绩的数据统计如下图所示，其中“理论部分”科目测试成绩为B的考生有10人．
（1）求该考场考生中“模拟现场”科目中成绩为A的人数；
（2）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分．
（i）求该考场考生“理论部分”科目的平均分；
（ii）若该考场共有10人得分大于7分，其中有2人10分，2人9分，6人8分．从这10人中随机抽取两人，求两人成绩之和的分布列和数学期望．

Answer 1

考点：离散型随机变量的期望与方差,众数、中位数、平均数

专题：概率与统计

分析：（1）由已知条件推导出该考场考生总人数为40人，由此能求出该考场考生中“模拟现场”科目中成绩为A的人数．
（2）（i）由频率分布直方图能求出该考场考生“理论部分”科目的平均分．
（ii）由题意知两人成绩之和X的可能取值为16，17，18，19，20，分别求出相对应的概率，由此能求出X的分布列EX．

解答： 解：（1）∵“理论部分”科目测试成绩为B的考生有10人，
∴该考场考生总人数为

10

0.25

=40人，
∴该考场考生中“模拟现场”科目中成绩为A的人数为40×0.075=3人．
（2）（i）该考场考生“理论部分”科目的平均分为：
0.075×5+0.25×4+0.375×3+（1-0.075-0.25-0.375-0.2）×2+0.2×1=2.9（分）．
（ii）由题意知两人成绩之和X的可能取值为16，17，18，19，20，
P（X=16）

C 2 6

C 2 10

=

1

3

，
P（X=17）=

C 1 6 C 1 2

C 2 10

=

4

15

，
P（X=18）=

C 2 2

C 2 10

+

C 1 2 C 1 6

C 2 10

=

13

45

，
P（X=19）=

C 1 2 C 1 2

C 2 10

=

4

45

，
P（X=20）=

C 2 2

C 2 10

=

1

45

，
∴X的分布列为：

X	16	17	18	19	20
P	1 3	4 15	13 45	4 45	1 45

EX=16×

1

3

+17×

4

15

+18×

13

45

+19×

4

45

+20×

1

45

=

86

5

．

点评：本题考查频率分布直方图的应用，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，注意排列组合知识的合理运用．