题目内容
1.在直角坐标系中,直线l过定点(-1,0),且倾斜角为α(0<α<π),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ=cosθ(ρcosθ+8).(1)写出l的参数方程和C的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,且$|AB|=8\sqrt{10}$,求α的值.
分析 (1)由直线l过定点(-1,0),且倾斜角为α(0<α<π),能求出l的参数方程;曲线C的极坐标方程转化为ρ2=ρ2cos2θ+8ρcosθ,由此能求出曲线C的直角坐标方程.
(2)把直线方程代入抛物线方程得:t2sin2α-8tcosα+8=0,从而${t_1}+{t_2}=\frac{8cosα}{{{{sin}^2}α}},{t_1}{t_2}=\frac{8}{{{{sin}^2}α}}$,由此利用$|AB|=8\sqrt{10}$,能求出α的值.
解答 解:(1)∵直线l过定点(-1,0),且倾斜角为α(0<α<π),
∴l的参数方程为$l:\left\{{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}}\right.$,(α为参数),
∵曲线C的极坐标方程为ρ=cosθ(ρcosθ+8).
∴ρ2=ρ2cos2θ+8ρcosθ,
∴曲线C的直角坐标方程为:y2=8x.
(2)把直线方程代入抛物线方程得:t2sin2α-8tcosα+8=0,
∴${t_1}+{t_2}=\frac{8cosα}{{{{sin}^2}α}},{t_1}{t_2}=\frac{8}{{{{sin}^2}α}}$,
∵$|AB|=8\sqrt{10}$,
∴$|{AB}|=|{{t_1}-{t_2}}|=\sqrt{{{({{t_1}+{t_2}})}^2}-4{t_1}{t_2}}=\frac{{4\sqrt{4-6{{sin}^2}α}}}{{{{sin}^2}α}}=8\sqrt{10}$,
∴20sin4α+3sin2α-2=0,∴${sin^2}α=\frac{1}{4}$,
∴$sinα=\frac{1}{2}∴α=\frac{π}{6}或α=\frac{5π}{6}$.
点评 本题考查直线的参数方程和曲线的直角坐标方程的求法,考查线段长的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案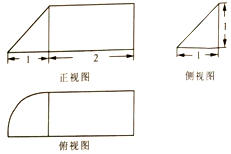
| A. | $\frac{1}{3}+\frac{π}{12}$ | B. | $1+\frac{π}{12}$ | C. | $\frac{1}{3}+\frac{π}{4}$ | D. | $1+\frac{π}{4}$ |
| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 关于直线y=x对称 |
| A. | $(-ln2,-\frac{1}{3}ln6]$ | B. | $(-\frac{1}{e},-\frac{ln6}{3}]$ | C. | $[\frac{1}{3}ln6,ln2)$ | D. | $[\frac{ln6}{3},\frac{2}{e})$ |
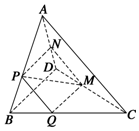 如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).
如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).