题目内容
9．已知是某几何体的三视图，则该几何体的体积为（ ）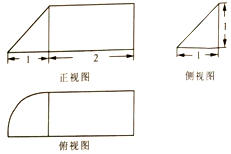
| A． | $\frac{1}{3}+\frac{π}{12}$ | B． | $1+\frac{π}{12}$ | C． | $\frac{1}{3}+\frac{π}{4}$ | D． | $1+\frac{π}{4}$ |
分析 由三视图可知：该几何体由圆锥的$\frac{1}{4}$与一个三棱柱组成的．
解答 解：由三视图可知：该几何体由圆锥的$\frac{1}{4}$与一个三棱柱组成的．
∴该几何体的体积V=$\frac{1}{4}×\frac{1}{3}×π×{1}^{2}×1$+$\frac{1}{2}×{1}^{2}×2$=1+$\frac{π}{12}$．
故选：B．
点评 本题考查了圆锥与三棱柱的三视图、体积计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
17．已知实数x，y满足条件$\left\{\begin{array}{l}{4x-y-8≤0}\\{2x-3y+6≥0}\\{x+y-2≥0}\end{array}\right.$，若x2+2y2≥m恒成立，则实数m的最大值为（ ）
| A． | 5 | B． | $\frac{4}{3}$ | C． | $\sqrt{2}$ | D． | $\frac{8}{3}$ |
4．已知曲线C：y=sin（2x+φ）（|φ|＜$\frac{π}{2}$）的一条对称轴方程为x=$\frac{π}{6}$，曲线C向左平移θ（θ＞0）个单位长度，得到的曲线E的一个对称中心为（$\frac{π}{6}$，0），则|φ-θ|的最小值是（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{12}$ |
14．某校高一（1）（2）两个班联合开展“诗词大会进校园，国学经典润心田”古诗词竞赛主题班会活动，主持人从这两个班分别随机选出20名同学进行当场测试，他们的测试成绩按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）分组，分别用频率分布直方图与茎叶图统计如图（单位：分）：
（2）班20名学生成绩茎叶图：
（Ⅰ）分别计算两个班这20名同学的测试成绩在[80，90）的频率，并补全频率分布直方图；
（Ⅱ）分别从两个班随机选取1人，设这两人中成绩在[80，90）的人数为X，求X的分布列（频率当作概率使用）．
（Ⅲ）运用所学统计知识分析比较两个班学生的古诗词水平．
（2）班20名学生成绩茎叶图：
| 4 | 5 |
| 5 | 2 |
| 6 | 4 5 6 8 |
| 7 | 0 5 5 8 8 8 8 9 |
| 8 | 0 0 5 5 |
| 9 | 4 5 |
（Ⅱ）分别从两个班随机选取1人，设这两人中成绩在[80，90）的人数为X，求X的分布列（频率当作概率使用）．
（Ⅲ）运用所学统计知识分析比较两个班学生的古诗词水平．
18．已知全集U，集合M，N满足M⊆N⊆U，则下列结论正确的是（ ）
| A． | M∪N=U | B． | （∁UM）∪（∁UN）=U | C． | M∩（∁UN）=∅ | D． | （∁UM）∪（∁UN）=∅ |
19．已知e为自然对数的底，a=（$\frac{2}{e}$）-0.2，b=（$\frac{e}{2}$）0.4，c=$lo{g}_{\frac{2}{e}}e$，则a，b，c的大小关系是（ ）
| A． | c＜a＜b | B． | c＜b＜a | C． | b＜a＜c | D． | a＜b＜c |