题目内容
10.已知函数f(x)=$\frac{ln(2x)}{x}$,关于x的不等式f2(x)+af(x)>0只有两个整数解,则实数a的取值范围是( )| A. | $(-ln2,-\frac{1}{3}ln6]$ | B. | $(-\frac{1}{e},-\frac{ln6}{3}]$ | C. | $[\frac{1}{3}ln6,ln2)$ | D. | $[\frac{ln6}{3},\frac{2}{e})$ |
分析 判断f(x)的单调性,作出f(x)的图象,利用函数图象得出a的范围.
解答 解:f′(x)=$\frac{1-ln(2x)}{{x}^{2}}$,令f′(x)=0得x=$\frac{e}{2}$,
∴当0<x<$\frac{e}{2}$时,f′(x)>0,f(x)单调递增,
当x>$\frac{e}{2}$时,f′(x)<0,f(x)单调递减,
由当x$<\frac{1}{2}$时,f(x)<0,当x$>\frac{1}{2}$时,f(x)>0,
作出f(x)的大致函数图象如图所示: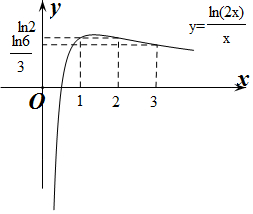
∵f2(x)+af(x)>0,
(1)若a=0,即f2(x)>0,显然不等式有无穷多整数解,不符合题意;
(2)若a>0,则f(x)<-a或x>0,
由图象可知f(x)>0有无穷多整数解,不符合题意;
(3)若a<0,则f(x)<0或f(x)>-a,
由图象可知f(x)<0无整数解,故f(x)>-a有两个整数解,
∵f(1)=f(2)=ln2,且f(x)在($\frac{e}{2}$,+∞)上单调递减,
∴f(x)>-a的两个整数解必为x=1,x=2,
又f(3)=$\frac{ln6}{3}$,
∴$\frac{ln6}{3}$≤-a<ln2,解得-ln2<a≤-$\frac{ln6}{3}$.
故选:A.
点评 本题考查了函数的单调性判断,不等式的解与函数图象的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知全集U,集合M,N满足M⊆N⊆U,则下列结论正确的是( )
| A. | M∪N=U | B. | (∁UM)∪(∁UN)=U | C. | M∩(∁UN)=∅ | D. | (∁UM)∪(∁UN)=∅ |
15.已知函数F(x)=f(x)+x2是奇函数,且f(2)=1,则f(-2)=( )
| A. | 9 | B. | -9 | C. | -7 | D. | 7 |
2.已知集合A={x|x2+x-6>0},集合B={x|-1<x<3},若a∈(A∪B),则a可以是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
19.已知e为自然对数的底,a=($\frac{2}{e}$)-0.2,b=($\frac{e}{2}$)0.4,c=$lo{g}_{\frac{2}{e}}e$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | a<b<c |
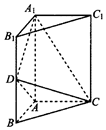 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.