题目内容
16.函数$f(x)=\frac{1}{x}{log_2}({{4^x}+1})-1$的图象( )| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 关于直线y=x对称 |
分析 根据对数运算性质、指数运算性质化简f(x),f(-x),判断f(x)的奇偶性,即可得出结论.
解答 解:f(x)=$\frac{1}{x}$log2(4x+1)-1=log2(4x+1)${\;}^{\frac{1}{x}}$-1=log2$\frac{({4}^{x}+1)^{\frac{1}{x}}}{2}$,
f(-x)=log2$\frac{({4}^{-x}+1)^{-\frac{1}{x}}}{2}$=log2$\frac{1}{2•({4}^{-x}+1)^{\frac{1}{x}}}$=log2[$\frac{1}{2}•$($\frac{1}{{4}^{-x}+1}$)${\;}^{\frac{1}{x}}$]
=log2[$\frac{1}{2}$•($\frac{{4}^{x}}{1+{4}^{x}}$)${\;}^{\frac{1}{x}}$]=log2$\frac{2}{(1+{4}^{x})^{\frac{1}{x}}}$,
∴f(-x)=-f(x),
∴f(x)是奇函数,f(x)的函数图象关于原点对称.
故选A.
点评 本题考查了指数运算性质,对数运算性质,函数奇偶性的判断,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
4.已知曲线C:y=sin(2x+φ)(|φ|<$\frac{π}{2}$)的一条对称轴方程为x=$\frac{π}{6}$,曲线C向左平移θ(θ>0)个单位长度,得到的曲线E的一个对称中心为($\frac{π}{6}$,0),则|φ-θ|的最小值是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
6.设复数z满足(1+i)z=-2i,i为虚数单位,则z=( )
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
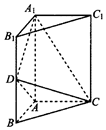 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.