题目内容
设函数f(x)=loga(1-ax),其中a>1.
(1)求函数f(x)的定义域,值域,并确定f(x)的图象在哪个象限;
(2)判断f(x)的单调性;
(3)证明y=f(x)的图象关于直线y=x对称;
(4)设方程f(x)+x+4=0有两个实数根x1,x2,求x1+x2.
(1)求函数f(x)的定义域,值域,并确定f(x)的图象在哪个象限;
(2)判断f(x)的单调性;
(3)证明y=f(x)的图象关于直线y=x对称;
(4)设方程f(x)+x+4=0有两个实数根x1,x2,求x1+x2.
考点:复合函数的单调性,函数的定义域及其求法,函数的值域,函数的图象与图象变化
专题:函数的性质及应用
分析:(1)由函数的解析式可得1-ax>0,求得的范围,可得函数的定义域.由1-ax <1,求得f(x)的值域.再根据函数的定义域和值域可得函数的图象位于第三象限.
(2)根据a>1,函数t=1-ax是(-∞,0)上的减函数,可得f(x)=loga(1-ax)的单调性.
(3)求得函数f(x)的反函数还是它本身,可得函数f(x)的图象关于直线y=x对称.
(4)由题意可得loga(1-ax)+x+4=0有两个实数根,化简可得 a4•ax-a4•a2x-1=0 有两个实数根.设这两个实数根为x1、x2,利用韦达定理可得ax1•ax2=
即 ax1+x2=a-4,从而求得x1+x2 的值.
(2)根据a>1,函数t=1-ax是(-∞,0)上的减函数,可得f(x)=loga(1-ax)的单调性.
(3)求得函数f(x)的反函数还是它本身,可得函数f(x)的图象关于直线y=x对称.
(4)由题意可得loga(1-ax)+x+4=0有两个实数根,化简可得 a4•ax-a4•a2x-1=0 有两个实数根.设这两个实数根为x1、x2,利用韦达定理可得ax1•ax2=
| 1 |
| a4 |
解答:
解:(1)由于f(x)=loga(1-ax),其中a>1,
由1-ax>0,求得x<0,故函数的定义域为(-∞,0).
由1-ax <1,可得f(x)<loga1=0,故函数的值域为(-∞,0).
再根据函数的定义域和值域可得函数的图象位于第三象限.
(2)由于a>1,函数t=1-ax是(-∞,0)上的减函数,
故f(x)=loga(1-ax)是(-∞,0)上的减函数.
(3)令y=loga(1-ax),求得ax =1-ay,即x=loga(1-ay),
故函数f(x)的反函数为y=loga(1-ax).
再根据函数f(x)的反函数还是它本身,故函数f(x)的图象关于直线y=x对称.
(4)由题意可得loga(1-ax)+x+4=0有两个实数根,即1-ax=a-x-4 有两个实数根,
即 a4•ax-a4•a2x-1=0 有两个实数根.
设这两个实数根为x1、x2,则ax1+ax2=1,ax1•ax2=
,∴ax1+x2=a-4,
∴x1+x2 =-4.
由1-ax>0,求得x<0,故函数的定义域为(-∞,0).
由1-ax <1,可得f(x)<loga1=0,故函数的值域为(-∞,0).
再根据函数的定义域和值域可得函数的图象位于第三象限.
(2)由于a>1,函数t=1-ax是(-∞,0)上的减函数,
故f(x)=loga(1-ax)是(-∞,0)上的减函数.
(3)令y=loga(1-ax),求得ax =1-ay,即x=loga(1-ay),
故函数f(x)的反函数为y=loga(1-ax).
再根据函数f(x)的反函数还是它本身,故函数f(x)的图象关于直线y=x对称.
(4)由题意可得loga(1-ax)+x+4=0有两个实数根,即1-ax=a-x-4 有两个实数根,
即 a4•ax-a4•a2x-1=0 有两个实数根.
设这两个实数根为x1、x2,则ax1+ax2=1,ax1•ax2=
| 1 |
| a4 |
∴x1+x2 =-4.
点评:本题主要考查复合函数的单调性,复合函数的定义域和值域,二次函数的性质、韦达定理,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
已知集合P={x|x2-2x-3>0},Q={x|log2(x-2)<1},则(∁RP)∩Q=( )
| A、{x|2<x≤3} |
| B、{x|-1≤x≤3} |
| C、{x|3<x≤4} |
| D、{x|3<x≤4或x<-1} |
 如图,半径都为1的三个圆两两相交,
如图,半径都为1的三个圆两两相交, |
| AB |
 |
| BC |
 |
| AC |
 |
| CD |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
曲线y=xn(x∈N)在点P(
,(
)n)处的切线的斜率为20,则n为( )
| 2 |
| 2 |
| A、7 | B、6 | C、5 | D、4 |
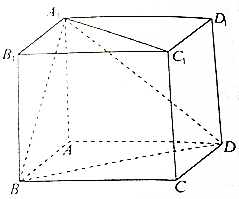 如图,正方体ABCD-A1B1C1D1的棱长为a,求:
如图,正方体ABCD-A1B1C1D1的棱长为a,求: