题目内容

设{bn}是递增的等差数列，已知b1+b2+b3=6，b1b2b3=
7
2
，求等差数列{bn}的通项．
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：设等差数列{bn}的公差是d，根据题意和等差数列的通项公式列出方程组，结合条件求出首项和公差，再求出等差数列{bn}的通项．
解答： 解：设等差数列{bn}的公差是d，
因为b1+b2+b3=6，b1b2b3=
7
2
，
所以
3b1+3d=6
b1(b1+d)(b1+2d)=
7
2
，
解得
b1=
1
2
d=
3
2
或
b1=
7
2
d=-
3
2
，
因为{bn}是递增的等差数列，
所以
b1=
1
2
d=
3
2
，
所以bn=
1
2
+（n-1）×
3
2
=
3n
2
-1．
点评：本题考查等差数列的通项公式，方程思想，以及化简计算能力，属于基础题．
练习册系列答案
相关题目
已知cos2α-cos2β=a，那么sin（α+β）sin（α-β）等于（　　）
A、-
a
2
B、
a
2
C、-a
D、a
已知函数f（x）满足f（x+1）=f（x）+1，当x∈[0，1]时，f（x）=|3x-1|-1，若对任意实数x，都有f（x+a）＜f（x）成立，则实数a的取值范围是
 
．
判断凼数y=cos2（x-
π
12
）+sin2（x+
π
12
）-1的奇偶性，并求周期．
已知在等差数列{an}中，a1=20，an=54，Sn=888，求n与d．
设函数f（x）=loga（1-ax），其中a＞1．
（1）求函数f（x）的定义域，值域，并确定f（x）的图象在哪个象限；
（2）判断f（x）的单调性；
（3）证明y=f（x）的图象关于直线y=x对称；
（4）设方程f（x）+x+4=0有两个实数根x1，x2，求x1+x2．
已知高为1的梯形ABCD内接于半径为1的圆O，若梯形的上底CD=1，则（
OA
+
OB
）•
OC
=（　　）
A、0
B、
3
2
C、
2
3
-3
2
D、
3-2
3
2
已知函数f（x）=ax2+
b
x
+5（其中常数a，b∈R）满足f（2）+f（-2）=26．
（Ⅰ）若f（-1）=-2000，求f（1）；
（Ⅱ）若函数φ（x）=xf（x）+2x+2-x（x∈（0，1））的值域为（0，
15
2
），求b的值；
（Ⅲ）在（Ⅱ）的条件下
①证明f（x）恰有一个零点；
②给出一个增函数g（x）使得当x∈N+时，g（x）∈N+，且
2
5
=rg（1）+rg（2）+rg（3）+…+rg（n）+…成立．
（已知等式
1
1-q
=1+q+q2+…+qn-1+…对任意实数q∈（-1，1）恒成立）
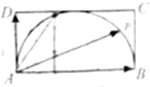如图，矩形ABCD中，AB=2AD=2，点P在以AB为直径的半圆上移动，若
AP
=λ
AB
+μ
AD
，则λ+μ的最大值是（　　）
A、
2
B、
2
+1
C、2
D、
5
+1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网