题目内容
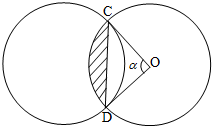
 如图,半径都为1的三个圆两两相交,
如图,半径都为1的三个圆两两相交, |
| AB |
 |
| BC |
 |
| AC |
 |
| CD |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:概率与统计
分析:根据
,
,
的长度相等,
的长度为
,可知
所对的圆心角α=
,从而可得图中阴影部分的面积为
π+3,空白部分面积为
,即得结论.
 |
| AB |
 |
| BC |
 |
| AC |
 |
| CD |
| π |
| 2 |
 |
| CD |
| π |
| 2 |
| 3 |
| 2 |
2
| ||
| 4 |
解答:
 解:如图:因为
解:如图:因为
=α•R=
,所以α=
,
故图中阴影部分的面积为
-
.
所以可得原题中阴影部分的面积为3π-3[2(
-
)]=
π+3.
又因为
,
,
的长度相等,
故△ABC为等边三角形,
则∠EBC=∠BCD=
,
又∠OCD=
,
所以∠OCB=∠OCD-∠BCD=
-
=
,
从而∠BOC=∠EBC-∠OCB=
-
=
,
所以BO=BC=AB=AC,
设其长度为x,则CE=
,BE=
x,
由于△COE为直角三角形,
所以
2=
2+
2,
即1=
+(x+
x)2,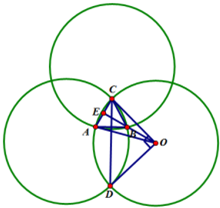
解得x2=2-
.
所以原图内部空白区域的面积为
S△ABC+3S弓=
×(2-
)×
+3×(
×
-
×
)
=
×(2-
)+
=
.
所以整个图形的面积为
+
π+3=
.
故所求概率为
=
.
故选D.
 解:如图:因为
解:如图:因为 |
| CD |
| π |
| 2 |
| π |
| 2 |
故图中阴影部分的面积为
| π |
| 4 |
| 1 |
| 2 |
所以可得原题中阴影部分的面积为3π-3[2(
| π |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
又因为
 |
| AB |
 |
| BC |
 |
| AC |
故△ABC为等边三角形,
则∠EBC=∠BCD=
| π |
| 6 |
又∠OCD=
| π |
| 4 |
所以∠OCB=∠OCD-∠BCD=
| π |
| 4 |
| π |
| 6 |
| π |
| 12 |
从而∠BOC=∠EBC-∠OCB=
| π |
| 6 |
| π |
| 12 |
| π |
| 12 |
所以BO=BC=AB=AC,
设其长度为x,则CE=
| x |
| 2 |
| ||
| 2 |
由于△COE为直角三角形,
所以
|
|
|
即1=
| x2 |
| 4 |
| ||
| 2 |

解得x2=2-
| 3 |
所以原图内部空白区域的面积为
S△ABC+3S弓=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 4 |
| 3 |
| π-3 |
| 4 |
=
2
| ||
| 4 |
所以整个图形的面积为
2
| ||
| 4 |
| 3 |
| 2 |
2
| ||
| 4 |
故所求概率为
| ||||
|
| 6π+12 | ||
7π+2
|
故选D.
点评:本题考查弧长公式,考查扇形的面积公式.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目