题目内容
10.函数f(x)=ln(x2-2x-3)的单调递增区间是(3,+∞).分析 令t=x2-2x-3>0 求得函数的定义域,结合f(x)=g(t)=lnt,本题即求二次函数t在定义域内的增区间,再利用二次函数的性质可得得出结论.
解答 解:令t=x2-2x-3>0,求得x<-1,或 x>3,故函数的定义域为{x|x<-1,或 x>3 }.
根据f(x)=g(t)=lnt,本题即求二次函数t在定义域内的增区间.
再利用二次函数的性质可得函数t在定义域内的增区间为(3,+∞),
故答案为:(3,+∞).
点评 本题主要考查复合函数的单调性,对数函数、二次函数的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
6.已知角α是第四象限角,角α的终边经过点P(4,y),且sinα=$\frac{y}{5}$,则tanα的值是( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
20.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1>0}\\{x<2}\\{x+y-1>0}\end{array}\right.$,若z=2x-2y-1,则z的取值范围为( )
| A. | (-$\frac{5}{3}$,5) | B. | (-$\frac{5}{3}$,0) | C. | [0,5] | D. | [-$\frac{5}{3}$,5] |
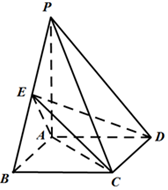 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.