题目内容
20.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1>0}\\{x<2}\\{x+y-1>0}\end{array}\right.$,若z=2x-2y-1,则z的取值范围为( )| A. | (-$\frac{5}{3}$,5) | B. | (-$\frac{5}{3}$,0) | C. | [0,5] | D. | [-$\frac{5}{3}$,5] |
分析 根据画出不等式组表示的平面区域,利用数形结合结合目标函数的意义,利用平移即可得到结论
解答 解:不等式对应的平面区域如图:(阴影部分).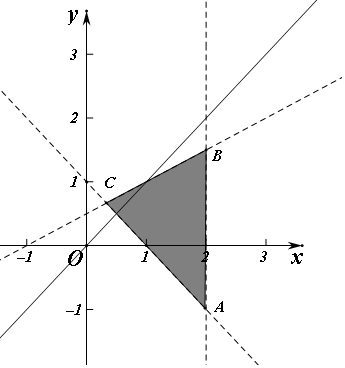
由z=2x-2y-1得y=x-$\frac{1+z}{2}$,平移直线y=x-$\frac{1+z}{2}$,
由平移可知当直线y=x-$\frac{1+z}{2}$,经过点A(2,-1)时,
直线y=x-$\frac{1+z}{2}$的截距最小,此时z取得最大值,
此时z=2x-2y-1=4+2-1=5,
可知当直线y=x-$\frac{1+z}{2}$,经过点C时,
直线y=x-$\frac{1+z}{2}$的截距最大,此时z取得最小值,
由$\left\{\begin{array}{l}{x-2y+1=0}\\{x+y-1=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,即A($\frac{1}{3}$,$\frac{2}{3}$)
代入z=2x-2y-1得z=2×$\frac{1}{3}$-2×$\frac{2}{3}$-1=-$\frac{5}{3}$,
故z∈(-$\frac{5}{3}$,5).
故选:A.
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在等差数列{an}中,若a1+a5+a9=$\frac{π}{2}$,则sin(a4+a6)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
15.过双曲线的一个焦点F2作垂直干实轴的弦PQ,F1是另一焦点,若∠PF1Q=$\frac{π}{2}$,则双曲线的离心率e等于( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | $\sqrt{2}$+1 |
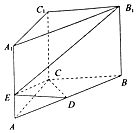 如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).
如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R). 如图,茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员的平均成绩相同,则成绩较为稳定的运动员成绩的方差为2.
如图,茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员的平均成绩相同,则成绩较为稳定的运动员成绩的方差为2.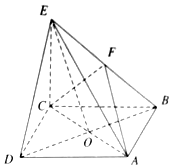 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.