题目内容
19.在平面直角坐标系xoy中,已知直线l:ax+y+2=0和点A(-3,0),若直线l上存在点M满足MA=2MO,则实数a的取值范围为a≤0,或a≥$\frac{4}{3}$.分析 取M(x,-2-ax),直线l上存在点M满足MA=2MO,可得$\sqrt{(x+3)^{2}+(-2-ax)^{2}}$=2$\sqrt{{x}^{2}+(-2-ax)^{2}}$,化为:(a2+1)x2+(4a-2)x+1=0,此方程有实数根,可得△≥0,解出即可得出.
解答 解:取M(x,-2-ax),
∵直线l上存在点M满足MA=2MO,
∴$\sqrt{(x+3)^{2}+(-2-ax)^{2}}$=2$\sqrt{{x}^{2}+(-2-ax)^{2}}$,
化为:(a2+1)x2+(4a-2)x+1=0,此方程有实数根,
∴△=(4a-2)2-4(a2+1)≥0,
化为3a2-4a≥0,
解得a≤0,或a≥$\frac{4}{3}$.
故答案为:a≤0,或a≥$\frac{4}{3}$.
点评 本题考查了两点之间的距离公式、一元二次方程的实数解与判别式的关系、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9.“a<0”是函数“函数f(x)=|x-a|+|x|在区间[0,+∞)上为增函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.在等差数列{an}中,若a1+a5+a9=$\frac{π}{2}$,则sin(a4+a6)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
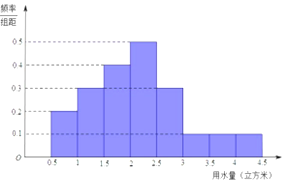 某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:
某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图: