题目内容
为了测试某批灯光的使用寿命,从中抽取了20个灯泡进行试验,记录如下:(以小时为单位)
171 159、168、166、170、158、169、166、165、162
168 163、172、161、162、167、164、165、164、167
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)从频率分布的直方图中,估计这些灯泡的使用寿命.
171 159、168、166、170、158、169、166、165、162
168 163、172、161、162、167、164、165、164、167
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)从频率分布的直方图中,估计这些灯泡的使用寿命.
考点:频率分布直方图,频率分布表
专题:计算题,概率与统计
分析:(1)由题意组距为5小时,作出样本频率分布表.
(2)利用样本频率分布表,以横轴表示时间,纵轴表示
,能作出频率分布直方图.
(3)利用组中值计算这些灯泡的使用寿命.
(2)利用样本频率分布表,以横轴表示时间,纵轴表示
| 频率 |
| 组距 |
(3)利用组中值计算这些灯泡的使用寿命.
解答:
解:(1)由题意组距为5小时,作出样本频率分布表:
(2)频率分布直方图为:

(3)这些灯泡的使用寿命160.5×0.25+165.5×0.45+170.5×0.3=165.75.
| 组别 | 频数 | 频率 |
| [158,163) | 5 | 0.25 |
| [163,168) | 9 | 0.45 |
| [168,173) | 6 | 0.3 |

(3)这些灯泡的使用寿命160.5×0.25+165.5×0.45+170.5×0.3=165.75.
点评:本题考查样本频率分布表和频率分布直方图的作法,是基础题,解题时要认真审题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在数列{an}中,a1=14,3an=3an+1+2,则使anan+2<0成立的n值是( )
| A、19 | B、20 | C、21 | D、22 |
若θ为三角形的一个内角,且sinθ+cosθ=
,则曲线 x2sinθ+y2cosθ=1是( )
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在y轴上的双曲线 |
| C、焦点在x轴上的椭圆 |
| D、焦点在y轴上的椭圆 |
下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能得出AB∥平面MNP的图形个数是( )
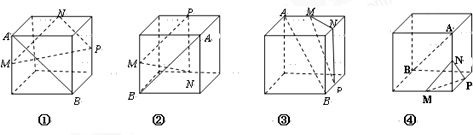

| A、1个 | B、2个 | C、3个 | D、4个 |
已知实数x,y满足x2+y2-4x+6y+4=0,则
的最小值是( )
|
A、2
| ||
B、
| ||
C、
| ||
D、
|