题目内容
若θ为三角形的一个内角,且sinθ+cosθ=
,则曲线 x2sinθ+y2cosθ=1是( )
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在y轴上的双曲线 |
| C、焦点在x轴上的椭圆 |
| D、焦点在y轴上的椭圆 |
考点:圆锥曲线的共同特征
专题:计算题,圆锥曲线的定义、性质与方程
分析:把sinθ+cosθ=
两边平方可得,sinθ•cosθ<0,可判断θ为钝角,cosθ<0,从而判断方程所表示的曲线.
| 1 |
| 5 |
解答:
解:因为θ∈(0,π),且sinθ+cosθ=
,所以θ∈(
,π),
且|sinθ|>|cosθ|,从而sinθ>cosθ<0,
从而x2sinθ+y2cosθ=1表示焦点在xy轴上的双曲线.
故选B.
| 1 |
| 5 |
| π |
| 2 |
且|sinθ|>|cosθ|,从而sinθ>cosθ<0,
从而x2sinθ+y2cosθ=1表示焦点在xy轴上的双曲线.
故选B.
点评:本题考查圆锥曲线的共同特征,由三角函数式判断角的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知向量
=(2,1),
=(x,-2)且
与
平行,则实数x的值等于( )
| a |
| b |
| a |
| b |
| A、-1 | B、1 | C、-4 | D、4 |
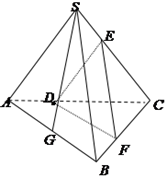 如图,在三棱锥S-ABC中,D、E、F分别是棱AC、BC、SC上的点,且CD=2DA,CE=2ES,CF=2FB,G是AB的中点.求证:SG∥平面DEF.
如图,在三棱锥S-ABC中,D、E、F分别是棱AC、BC、SC上的点,且CD=2DA,CE=2ES,CF=2FB,G是AB的中点.求证:SG∥平面DEF.