题目内容
(本小题满分14分)已知函数 ,
,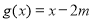 ,其中
,其中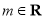 ,
, 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当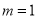 时,求函数
时,求函数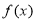 的极小值;
的极小值;
(Ⅱ)对 ,是否存在
,是否存在 ,使得
,使得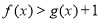 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)设 ,当
,当 时,若函数
时,若函数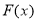 存在
存在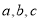 三个零点,且
三个零点,且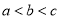 ,求证:
,求证:  .
.
(Ⅰ)1-ln2;(Ⅱ) ;(Ⅲ)见解析
;(Ⅲ)见解析
【解析】
试题分析:(Ⅰ)直接利用导数可得单调区间和极小值;(Ⅱ)函数存在三个零点,表示极大值g(0)大于零而极小值g(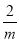 )小于零,得到m的范围,进而得到g(-1)和g(e)的范围,由此得出a,b,c满足的不等关系;(Ⅲ)由题意,
)小于零,得到m的范围,进而得到g(-1)和g(e)的范围,由此得出a,b,c满足的不等关系;(Ⅲ)由题意, ,而
,而 ,
, ,∴
,∴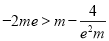 ,解出m的范围即可.
,解出m的范围即可.
试题解析:(Ⅰ)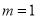 时,
时, .
.
∴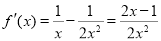 1分
1分
由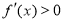 ,解得
,解得 ;由
;由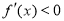 ,解得
,解得 ;
;
∴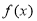 在
在 上单调递减,
上单调递减, 上单调递增. 2分
上单调递增. 2分
∴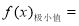
 . 2分
. 2分
(Ⅱ)令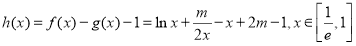 ,其中
,其中
由题意,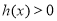 对
对 恒成立,
恒成立,
∵
∵ ,∴在二次函数
,∴在二次函数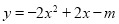 中,
中,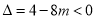 ,
,
∴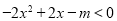 对
对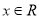 恒成立
恒成立
∴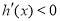 对
对 恒成立, ∴
恒成立, ∴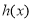 在
在 上单减.
上单减.
∴ ,即
,即 .
.
故存在 使
使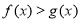 对
对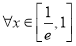 恒成立. 4分
恒成立. 4分
(Ⅲ) ,易知
,易知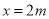 为函数
为函数 的一个零点,
的一个零点,
∵ ,∴
,∴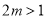 ,因此据题意知,函数
,因此据题意知,函数 的最大的零点
的最大的零点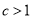 ,
,
下面讨论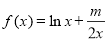 的零点情况,
的零点情况,
∵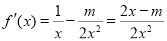 .
.
易知函数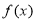 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
由题知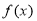 必有两个零点,
必有两个零点,
∴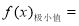
 ,解得
,解得 ,
,
∴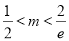 ,即
,即 . 3分
. 3分
∴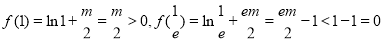 . 1分
. 1分
又 .
.
 .
.
 .
.
 ,得证. 1分
,得证. 1分
考点:利用导数研究函数性质,函数的单调性,极值,范围问题,恒成立问题

练习册系列答案
相关题目
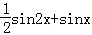 ,则f′(x)是( )
,则f′(x)是( )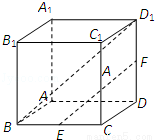
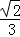 B.
B.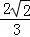 C.
C.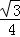 D.
D.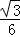
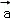 ,
,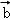 ,
,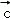 }是空间的一组单位正交基底,而{
}是空间的一组单位正交基底,而{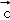 ,
, +
+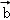 }是空间的另一组基底.若向量
}是空间的另一组基底.若向量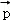 在基底{
在基底{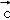 ,
,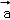 +
+ }下的坐标为( )
}下的坐标为( )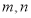 .
.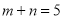 ”的概率;
”的概率;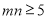 ”的概率.
”的概率.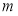 ,
,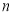 是两条不同直线,
是两条不同直线,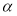 ,
,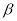 是两个不同的平面,且
是两个不同的平面,且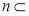
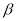 ,则下列叙述正确的是
,则下列叙述正确的是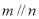 ,
,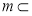
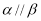
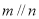
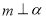 ,则
,则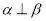
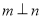 ,则
,则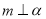
 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则
,则 __________.
__________.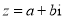
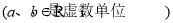 ,
,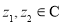 ,定义:
,定义: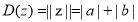 ,
,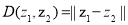 .给出下列命题:
.给出下列命题: 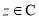 ,都有
,都有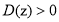 ;
;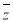 是复数
是复数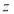 的共轭复数,则
的共轭复数,则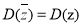 恒成立;
恒成立;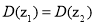
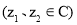 ,则
,则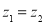 ;
;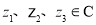 ,结论
,结论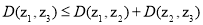 恒成立,则其中真命题是[答]( ).
恒成立,则其中真命题是[答]( ).