题目内容
已知{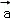 ,
,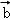 ,
,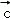 }是空间的一组单位正交基底,而{
}是空间的一组单位正交基底,而{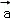 ﹣
﹣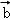 ,
,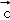 ,
, +
+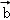 }是空间的另一组基底.若向量
}是空间的另一组基底.若向量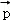 在基底{
在基底{ ,
,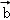 ,
,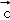 }下的坐标为(6,4,2),则向量
}下的坐标为(6,4,2),则向量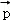 在基底{
在基底{ ﹣
﹣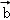 ,
,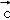 ,
,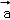 +
+ }下的坐标为( )
}下的坐标为( )
A.(1,2,5) B.(5,2,1) C.(1,2,3) D.(3,2,1)
A
【解析】
试题分析:设向量 在基底{
在基底{ ﹣
﹣ ,
, ,
, +
+ }下的坐标为(x,y,z),由
}下的坐标为(x,y,z),由 =6
=6 +4
+4 +2
+2 =x(
=x( ﹣
﹣ )+y
)+y +z(
+z( +
+ ),列出方程组,求出x,y,z的值即可.
),列出方程组,求出x,y,z的值即可.
【解析】
设向量 在基底{
在基底{ ﹣
﹣ ,
, ,
, +
+ }下的坐标为(x,y,z),
}下的坐标为(x,y,z),
可得 =6
=6 +4
+4 +2
+2 =x(
=x( ﹣
﹣ )+y
)+y +z(
+z( +
+ ),
),
所以:
∴x=1,y=2,z=5
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B.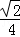 C.
C.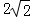 D.
D.
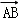 的坐标为 .
的坐标为 . ,
,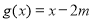 ,其中
,其中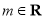 ,
, 为自然对数的底数.
为自然对数的底数.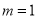 时,求函数
时,求函数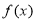 的极小值;
的极小值; ,是否存在
,是否存在 ,使得
,使得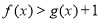 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由; ,当
,当 时,若函数
时,若函数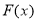 存在
存在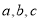 三个零点,且
三个零点,且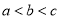 ,求证:
,求证:  .
. 的不等式
的不等式 的解集为
的解集为 ,集合
,集合 .若“
.若“ ”是“
”是“ ”的充分不必要条件,则实数
”的充分不必要条件,则实数 的取值范围是__________..
的取值范围是__________.. 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 满足
满足 ,
, .
. .
. ,
, ,
, 的前
的前 项和
项和 .
. ,点
,点 点
点 与点
与点 关于直线
关于直线 对称,且
对称,且 .直线
.直线 是过点
是过点 的任意一条直线.
的任意一条直线. 所在曲线
所在曲线 的轨迹方程;
的轨迹方程; 两点,且
两点,且 ,求直线
,求直线 两点,与线段
两点,与线段 交于点
交于点 (点
(点 ),直线
),直线 与直线
与直线 交于点
交于点 ,求证:
,求证: 是定值.
是定值.