题目内容
将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD中点,则∠AED的大小为( )
A.45° B.30° C.60° D.90°
D
【解析】
试题分析:由题意画出几何体的图形,设出正方形的边长,求出折叠后AD,AE,DE的长度,即可求出∠AED的大小.
【解析】
由题意画出图形,如图,
设正方形的边长为:2,
折叠前后AD=2,DE=1,连接AC交BD于O,连接OE,则OE=1,AO= ,
,
因为正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,
AO⊥BD,所以AO⊥平面BCD,所以AO⊥OE,
在△AOE中,AE= =
= ,
,
又AD=2,ED=1,所以DE2+AE2=AD2,
所以∠AED=90°.
故选D.


练习册系列答案
相关题目
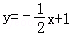
 的导数是( )
的导数是( ) B.﹣sinx C.
B.﹣sinx C. D.
D.
 B.
B.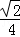 C.
C.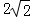 D.
D.
 ,
,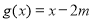 ,其中
,其中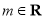 ,
, 为自然对数的底数.
为自然对数的底数.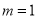 时,求函数
时,求函数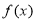 的极小值;
的极小值; ,是否存在
,是否存在 ,使得
,使得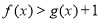 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由; ,当
,当 时,若函数
时,若函数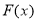 存在
存在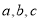 三个零点,且
三个零点,且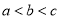 ,求证:
,求证:  .
. ,集合
,集合 ,则
,则 ( )
( ) (B)
(B)
 (D)
(D)