题目内容
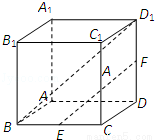
(2012•静安区一模)在棱长为1的正方体ABCD﹣A1B1C1D1中,E为棱BC的中点,F为棱DD1的中点.则异面直线EF与BD1所成角的余弦值是( )
A.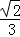 B.
B.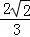 C.
C.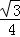 D.
D.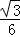
B
【解析】
试题分析:以AB、AD、AA1为x、y、z轴,建立空间直角坐标系如图,可得B、D1、E、F各点的坐标,从而得到 和
和 的长度和数量积,利用空间向量的夹角公式求出它们所成角的余弦,即可得到异面直线EF与BD1所成角的余弦值.
的长度和数量积,利用空间向量的夹角公式求出它们所成角的余弦,即可得到异面直线EF与BD1所成角的余弦值.
【解析】
以AB、AD、AA1为x、y、z轴,建立空间直角坐标系如图,
则B(1,0,0),D1(0,1,1),E(1, ,0),F(0,1,
,0),F(0,1, )
)
∴ =(﹣1,1,1),
=(﹣1,1,1), =(﹣1,
=(﹣1, ,
, )
)
可得 =
= ,
, =
=
 •
• =(﹣1)×(﹣1)+1×
=(﹣1)×(﹣1)+1× +1×
+1× =2
=2
设异面直线EF与BD1所成角为θ,则cosθ=| |=
|=
故选B


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的导数是( )
的导数是( ) B.﹣sinx C.
B.﹣sinx C. D.
D.
 B.
B.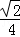 C.
C.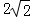 D.
D.
 ,
, ,则
,则 = .
= . ,
,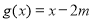 ,其中
,其中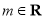 ,
, 为自然对数的底数.
为自然对数的底数.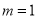 时,求函数
时,求函数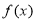 的极小值;
的极小值; ,是否存在
,是否存在 ,使得
,使得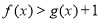 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由; ,当
,当 时,若函数
时,若函数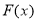 存在
存在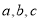 三个零点,且
三个零点,且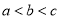 ,求证:
,求证:  .
. 的图象大致为( )
的图象大致为( )
 的顶点在坐标原点,始边与
的顶点在坐标原点,始边与 轴的正半轴重合,角
轴的正半轴重合,角 ,则
,则 = .(用数值表示)
= .(用数值表示)