题目内容
设f(x)=
,x1=1,xn=f(xn-1)(n≥2,n∈N*)
(1)求x2,x3,x4的值;
(2)归纳并猜想{xn}的通项公式;
(3)用数学归纳法证明你的猜想.
| 2x |
| x+2 |
(1)求x2,x3,x4的值;
(2)归纳并猜想{xn}的通项公式;
(3)用数学归纳法证明你的猜想.
考点:数学归纳法,归纳推理
专题:计算题,点列、递归数列与数学归纳法
分析:(1)利用f(x)=
,x1=1,xn=f(xn-1),计算可得x2,x3,x4的值;
(2)由(1)猜想{xn}的通项公式;
(3)利用数学归纳法证明步骤证明即可.
| 2x |
| x+2 |
(2)由(1)猜想{xn}的通项公式;
(3)利用数学归纳法证明步骤证明即可.
解答:
解:(1)∵f(x)=
,x1=1,xn=f(xn-1),
∴x2=f(x1)=
,x3=f(x2)=
,x4=f(x3)=
;
(2)猜想{xn}的通项公式xn=
;
(3)①n=1时,x1=
=1,成立;
②假设n=k时结论成立,即xk=
,则
xk+1=f(xk)=
=
,
∴n=k+1时,结论成立.
由①②可知xn=
.
| 2x |
| x+2 |
∴x2=f(x1)=
| 2 |
| 3 |
| 2 |
| 4 |
| 2 |
| 5 |
(2)猜想{xn}的通项公式xn=
| 2 |
| n+1 |
(3)①n=1时,x1=
| 2 |
| 1+1 |
②假设n=k时结论成立,即xk=
| 2 |
| k+1 |
xk+1=f(xk)=
2•
| ||
|
| 2 |
| (k+1)+1 |
∴n=k+1时,结论成立.
由①②可知xn=
| 2 |
| n+1 |
点评:本题考查归纳推理,数学归纳法,正确猜想,掌握数学归纳法的证明步骤是关键.

练习册系列答案
相关题目
已知平面α过点A(3,0,0),B(0,3,0),C(0,0,3),则原点O到平面α的距离为( )
| A、3 | ||
| B、6 | ||
C、
| ||
D、2
|
如图,PA是⊙O的切线,A为切点,PC是⊙O的割线,且PB=
BC,则
等于( )

| 1 |
| 2 |
| PA |
| PB |

| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
 在小时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是( )
在小时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是( )| A、大拇指 | B、食指 |
| C、中指 | D、无名指 |
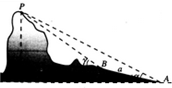 如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角β=15°的斜坡向上走100米到B,在B处测得山顶P的仰角为γ=60°,则山高h=
如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角β=15°的斜坡向上走100米到B,在B处测得山顶P的仰角为γ=60°,则山高h=