题目内容
已知函数f(x)=sin
,则f(1)+f(2)+…+f(2014)= .
| πx |
| 3 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:将x=1,2,3,4,5,…,2014分别代入f(x),归纳总结得到一般性规律,求出原式值即可.
解答:
解:当x=1时,f(1)=sin
=
;
当x=2时,f(2)=sin
=
;
当x=3时,f(3)=sinπ=0;
当x=4时,f(4)=sin
=-
;
当x=5时,f(5)=sin
=sin(2π-
)=-sin
=-
;
当x=6时,f(6)=sin2π=0;
当x=7时,f(7)=sin
=sin(2π+
)=sin
=
;
当x=8时,f(8)=sin
=sin(2π+
)=sin
=
;
…,
以此类推,其值以
,
,0,-
,-
循环,且之和为0,
∵2014÷5=402…4,
∴f(1)+f(2)+…+f(2014)=(
+
+0-
-
)+(
+
+0-
-
)+…+(
+
+0-
)=
.
故答案为:
| π |
| 3 |
| ||
| 2 |
当x=2时,f(2)=sin
| 2π |
| 3 |
| ||
| 2 |
当x=3时,f(3)=sinπ=0;
当x=4时,f(4)=sin
| 4π |
| 3 |
| ||
| 2 |
当x=5时,f(5)=sin
| 5π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
当x=6时,f(6)=sin2π=0;
当x=7时,f(7)=sin
| 7π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
当x=8时,f(8)=sin
| 8π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
…,
以此类推,其值以
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵2014÷5=402…4,
∴f(1)+f(2)+…+f(2014)=(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
在△ABC的三个内角之比为3:2:1,那么对应的三边之比为( )
| A、3:2:1 | ||||
B、
| ||||
C、
| ||||
D、2:
|
函数f(x)=
x-cosx的零点个数为( )
| 1 |
| 8 |
| A、3 | B、4 | C、5 | D、6 |
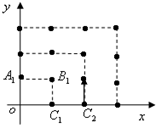 2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是