题目内容
已知函数f(x)=2
sinxcosx+2sin2x-1.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈[-
,
]时,求函数f(x)的取值范围.
| 3 |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈[-
| 5π |
| 12 |
| π |
| 6 |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:(Ⅰ)利用二倍角公式、辅助角公式化简函数,即可求函数f(x)的最小正周期;
(Ⅱ)当x∈[-
,
]时,可得2x-
∈[-π,
],利用正弦函数的性质,可求函数f(x)的取值范围.
(Ⅱ)当x∈[-
| 5π |
| 12 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:(Ⅰ)因为f(x)=2
sinxcosx+2sin2x-1=
sin2x-cos2x=2sin(2x-
),
所以函数f(x)的最小正周期T=
=π.…(7分)
(Ⅱ)因为x∈[-
,
],
所以2x-
∈[-π,
],
所以sin(2x-
)∈[-1,
],
所以2sin(2x-
)∈[-2,1],
所以函数f(x)的取值范围为[-2,1].…(13分)
| 3 |
| 3 |
| π |
| 6 |
所以函数f(x)的最小正周期T=
| 2π |
| 2 |
(Ⅱ)因为x∈[-
| 5π |
| 12 |
| π |
| 6 |
所以2x-
| π |
| 6 |
| π |
| 6 |
所以sin(2x-
| π |
| 6 |
| 1 |
| 2 |
所以2sin(2x-
| π |
| 6 |
所以函数f(x)的取值范围为[-2,1].…(13分)
点评:本题考查三角函数的化简,考查三角函数的性质,考查学生的计算能力,正确化简函数是关键.

练习册系列答案
相关题目
若函数f(x)=x2+a|x-1|(a∈R),则对不同的实数a,函数f(x)的单调区间的个数有可能的是( )
| A、1个或2个 |
| B、2个或3个 |
| C、3个或4个 |
| D、2个或4个 |
若圆(x-1)2+(y-2)2=5的圆心到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、-2或2 | ||
B、
| ||
| C、2或0 | ||
| D、-2或0 |
若直线x+y+a=0与圆(x-a)2+y2=2相切,则a=( )
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、1或-1 |
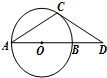 (几何证明选讲选做题)如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若
(几何证明选讲选做题)如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若 已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.
已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.