题目内容
17.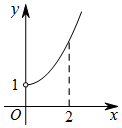 已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )| A. | $y=x+\frac{1}{x}$ | B. | y=log2|x| | ||
| C. | $y=\left\{{\begin{array}{l}{e^x}&{x≥0}\\{{e^{-x}}}&{x<0}\end{array}}\right.$ | D. | y=cos(2x) |
分析 根据题意,由函数奇偶性的性质分析可得y=f(x)在(-1,0)上单调递增,据此依次分析选项中函数在区间(-1,0)上的单调性,即可得答案.
解答 解:根据图象可以判断出(0,1)单调递增,又由函数y=f(x)(x∈R)是奇函数,
则函数y=f(x)在(-1,0)上单调递增,
依次分析选项:
对于A、对于y=x+$\frac{1}{x}$,y′=1-$\frac{1}{{x}^{2}}$=$\frac{{x}^{2}-1}{{x}^{2}}$,当-1<x<0时,y′<0,则f(x)在(-1,0)是减函数,不符合题意,
对于B、当-1<x<0时,y=log2|x|=log2(-x),令t=-x,则y=log2t,t=-x在(-1,0)为减函数,而y=log2t为增函数,则y=log2|x|在(-1,0)是减函数,不符合题意,
对于C、当-1<x<0时,y=e-x=($\frac{1}{e}$)x,而0<$\frac{1}{e}$<1,则y=e-x在(-1,0)为减函数,不符合题意,
对于D、y=cos(2x),当-1<x<0,则有-2<2x<0,y=cos(2x)为增函数,符合题意;
故选:D.
点评 本题考查函数奇偶性的性质,涉及函数单调性的判定,利用函数奇偶性和单调性的关系是解决本题的关键

练习册系列答案
相关题目
8.函数$f(x)=tan(2x-\frac{π}{6})$的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
12.已知函数f(x)=|x+3|+2,g(x)=kx+1,若方程f(x)=g(x)有两个不相等的实根,则实数a的取值范围是( )
| A. | (-$\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{3}$) | D. | (-1,-$\frac{1}{3}$) |
9.过抛物线y2=4x的焦点F的直线与其交于A,B两点,|AF|>|BF|,如果|AF|=5,那么|BF|=( )
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |