题目内容
5．在数列{an}中，若a1=1，an+1=2an+1（n≥1），则数列的通项an=2n-1．分析 利用递推关系式，推出数列{an+1}是等比数列，然后求解数列的通项公式即可．
解答 解：在数列{an}中，若a1=1，an+1=2an+1（n≥1），
可得an+1+1=2（an+1），可得数列{an+1}是以2为首项，2为公比的等比数列，
an+1=2•2n-1=2n．
数列的通项an=2n-1．
故答案为：2n-1．
点评 本题考查数列的递推关系式的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
11．（1+x）6（1+y）4的展开式中，记xmyn项的系数为f（m，n），则f（3，0）+f（0，3）=（ ）
| A． | 9 | B． | 16 | C． | 18 | D． | 24 |
13．已知函数f（x）=$\left\{\begin{array}{l}-{x^2}-ax-5，（x≤1）\\ \frac{a}{x}（x＞1）\end{array}$是R上的增函数，则a的取值范围是（ ）
| A． | {a|-3≤a＜0} | B． | {a|a≤-2} | C． | {a|a＜0} | D． | {a|-3≤a≤-2} |
10．下列命题中的假命题是（ ）
| A． | ?x∈R，log2x=0 | B． | ?x∈R，cosx=1 | C． | ?x∈R，x2＞0 | D． | ?x∈R，2x＞0 |
17．
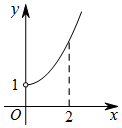已知函数y=f（x），x∈R是奇函数，其部分图象如图所示，则在（-1，0）上与函数f（x）的单调性相同的是（ ）
已知函数y=f（x），x∈R是奇函数，其部分图象如图所示，则在（-1，0）上与函数f（x）的单调性相同的是（ ）| A． | $y=x+\frac{1}{x}$ | B． | y=log2|x| | ||
| C． | $y=\left\{{\begin{array}{l}{e^x}&{x≥0}\\{{e^{-x}}}&{x＜0}\end{array}}\right.$ | D． | y=cos（2x） |