题目内容
9．过抛物线y2=4x的焦点F的直线与其交于A，B两点，|AF|＞|BF|，如果|AF|=5，那么|BF|=（ ）| A． | $\frac{{3\sqrt{5}}}{2}$ | B． | $\frac{5}{4}$ | C． | $\frac{5}{2}$ | D． | $\frac{3}{2}$ |
分析 根据抛物线的定义，结合|AF|=5，求出A的坐标，然后求出AF的方程求出B点的横坐标即可得到结论．
解答 
解：抛物线的焦点F（1，0），准线方程为x=-1，
设A（x，y），则|AF|=x+1=5，故x=4，此时y=4，
即A（4，4），
则直线AF的方程为$\frac{y-0}{4-0}$=$\frac{x-1}{4-1}$，即y=$\frac{4}{3}$（x-1），
代入y2=4x得4x2-17x+4=0，
解得x=4（舍）或x=$\frac{1}{4}$，
则|BF|=$\frac{1}{4}$+1=$\frac{5}{4}$，
故选B．
点评 本题考查抛物线的简单几何性质，考查抛物线的焦点弦长公式，考查数形结合思想，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．
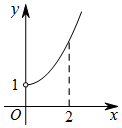已知函数y=f（x），x∈R是奇函数，其部分图象如图所示，则在（-1，0）上与函数f（x）的单调性相同的是（ ）
已知函数y=f（x），x∈R是奇函数，其部分图象如图所示，则在（-1，0）上与函数f（x）的单调性相同的是（ ）| A． | $y=x+\frac{1}{x}$ | B． | y=log2|x| | ||
| C． | $y=\left\{{\begin{array}{l}{e^x}&{x≥0}\\{{e^{-x}}}&{x＜0}\end{array}}\right.$ | D． | y=cos（2x） |
一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部（如图），已知目标函数z=3+ax+by（a，b∈R）的最大值只在顶点B处，如果目标函数变成z=3-bx-ay时，最大值只在顶点（ ）