题目内容
12.已知函数f(x)=|x+3|+2,g(x)=kx+1,若方程f(x)=g(x)有两个不相等的实根,则实数a的取值范围是( )| A. | (-$\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{3}$) | D. | (-1,-$\frac{1}{3}$) |
分析 画出函数f(x)、g(x)的图象,由题意可得函数f(x)的图象(蓝线)和函数g(x)的图象(红线)有两个交点,数形结合求得k的范围.
解答 解:由题意可得函数f(x)的图象(蓝线)
和函数g(x)的图象(红线)有两个交点,
如图所示:KBA=-$\frac{1}{3}$,
数形结合可得-1<k<-$\frac{1}{3}$,
故选:D.
点评 本题主要考查根的存在性及根的个数判断、考查函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
18.设抛物线的顶点在原点,其焦点在x轴上,又抛物线上的点A(-1,a)与焦点F的距离为2,则a=( )
| A. | 4 | B. | 4或-4 | C. | -2 | D. | -2或2 |
17.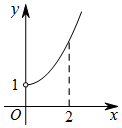 已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )
 已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )| A. | $y=x+\frac{1}{x}$ | B. | y=log2|x| | ||
| C. | $y=\left\{{\begin{array}{l}{e^x}&{x≥0}\\{{e^{-x}}}&{x<0}\end{array}}\right.$ | D. | y=cos(2x) |
4. 一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
 一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )| A. | A | B. | B | C. | C | D. | D |
2.如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的表面积是( )


| A. | $1+\sqrt{5}$ | B. | $2+\sqrt{5}$ | C. | $1+2\sqrt{5}$ | D. | $2+2\sqrt{5}$ |