题目内容
设z为虚数,且z+
+1=0.
(1)求z;
(2)求z+z2+z3+…+z2013的值;
(3)若复数z所对应的点在第二象限,w∈C,且1≤|w-4z|≤2,求|w|的范围.
| 1 |
| z |
(1)求z;
(2)求z+z2+z3+…+z2013的值;
(3)若复数z所对应的点在第二象限,w∈C,且1≤|w-4z|≤2,求|w|的范围.
考点:复数求模,复数代数形式的混合运算
专题:数系的扩充和复数
分析:(1)依题意,可得z2+z+1=0,从而可得z;
(2)依题意,可得z3=1,利用等比数列的求和公式即可求得z+z2+z3+…+z2013的值;
(3)利用1≤|w-4z|≤2表示的几何意义即可求得|w|的范围.
(2)依题意,可得z3=1,利用等比数列的求和公式即可求得z+z2+z3+…+z2013的值;
(3)利用1≤|w-4z|≤2表示的几何意义即可求得|w|的范围.
解答:
解:(1)∵z+
+1=0,
∴z2+z+1=0,解得z=-
±
i;
(2)∵z=-
±
i,
∴z3=1,又z2013=z671×3=1,{zn}为等比数列,
∴z+z2+z3+…+z2013=
=0;
(3)∵复数z所对应的点在第二象限,
∴z=-
+
i,又1≤|w-4z|≤2,
∴1≤|w-(-2+2
i)|≤2,w是以(-2,2
)为圆心,半径分别为2与1的圆环,
∴4-2≤|w|≤4+2,即2≤|w|≤6.
| 1 |
| z |
∴z2+z+1=0,解得z=-
| 1 |
| 2 |
| ||
| 2 |
(2)∵z=-
| 1 |
| 2 |
| ||
| 2 |
∴z3=1,又z2013=z671×3=1,{zn}为等比数列,
∴z+z2+z3+…+z2013=
| z(1-z2013) |
| 1-z |
(3)∵复数z所对应的点在第二象限,
∴z=-
| 1 |
| 2 |
| ||
| 2 |
∴1≤|w-(-2+2
| 3 |
| 3 |
∴4-2≤|w|≤4+2,即2≤|w|≤6.
点评:本题考查复数代数形式的混合运算,考查等比数列的求和公式及复数的几何意义,属于中档题.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
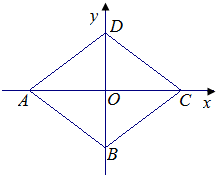 如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.
如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.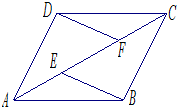 如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形.
如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形. 如图,是一个几何体的三视图,其中俯视图是正三角形,求:
如图,是一个几何体的三视图,其中俯视图是正三角形,求: