题目内容
设函数y=f(x)的定义域为(0,+∞),若对给定的正数K,定义fK(x)=
,则当函数f(x)=
,K=1时,
fK(x)dx= .
|
| 1 |
| x |
| ∫ | 2
|
考点:定积分
专题:导数的概念及应用
分析:根据fk(x)的定义求出fk(x)的表达式,然后根据积分的运算法则即可得到结论.
解答:
解:由定义可知当k=1时,f1(x)=
,即f1(x)=
,
则定积分
fK(x)dx=
dx+
1dx=lnx|
+x|
=ln1-ln
+2-1=1+2ln2,
故答案为:1+2ln2.
|
|
则定积分
| ∫ | 2
|
| ∫ | 1
|
| 1 |
| x |
| ∫ | 2 1 |
1
|
2 1 |
| 1 |
| 4 |
故答案为:1+2ln2.
点评:本题主要考查积分的计算,利用函数的定义求出函数的表达式是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
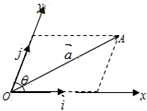 已知单位向量
已知单位向量