题目内容

已知z1，z2为共轭复数，且z1z2+（z1+z2）i=4-2i．求复数z1及它的模|z1|．
考点：复数求模
专题：数系的扩充和复数
分析：设出复数z1，z2，代入z1z2+（z1+z2）i=4-2i后整理，由复数相等的条件列式求得z1，代入复数模的计算公式求模．
解答： 解：设z1=x+yi（x，y∈R），则z2=x-yi，
z1z2+（z1+z2）i=x2+y2+2xi=4-2i，
∴
x2+y2=4
x=-1
，解得
x=-1
y=
3
或
x=-1
y=-
3
．
∴z1=-1±
3
i．
则|z1|=
(-1)2+(
3
)2
=2．
点评：本题考查了复数代数形式的乘除运算，考查了复数相等的条件，训练了复数模的求法，是基础题．
练习册系列答案
相关题目
用分析法证明：
a
-
a-1
＜
a-2
-
a-3
（a≥3）．
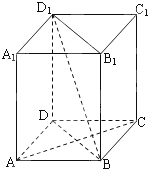如图，在四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，底面ABCD是正方形，且AB=1，D1D=
2
．
（1）求直线D1B与平面ABCD所成角的大小；
（2）求证：AC⊥平面BB1D1D．
已知数列{an}满足a1=5，a2=5，an+1=an+6an-1，（n≥2，n∈N*）．
（Ⅰ）求证数列{an+1+2an}是等比数列；
（Ⅱ）求出所有使数列{an+1+λan}成等比数列的λ的值；
（Ⅲ）求数列{an}的通项公式．
讨论函数y=x+
a
x
的定义域，值域，单调性．
设z为虚数，且z+
1
z
+1=0．
（1）求z；
（2）求z+z2+z3+…+z2013的值；
（3）若复数z所对应的点在第二象限，w∈C，且1≤|w-4z|≤2，求|w|的范围．
在△ABC中，A=45°，a=2，c=
6
，C=60°，
（Ⅰ）求△ABC的面积；
（Ⅱ）求
BA
•
BC
．
已知函数f（x）=x+alnx（a∈R）．
（I）若a=-1时，求曲线y=f（x）在点x=1处的切线方程；
（Ⅱ）若a≤0，函数f（x）没有零点，求a的取值范围．
已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于P，Q两点，O为坐标原点，若OP⊥OQ，则m的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网