题目内容
已知函数f(x)=ax2+lnx(a∈R)
(Ⅰ)当a=2时,求f(x)在区间[e,e2]上的最大值和最小值;
(Ⅱ)如果函数g(x),f1(x),f2(x)在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“伴随函数”.已知函数f1(x)=(a-
)x2+2ax+(1-a2)lnx,f2(x)=
x2+2ax.若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,求a的取值范围.
(Ⅰ)当a=2时,求f(x)在区间[e,e2]上的最大值和最小值;
(Ⅱ)如果函数g(x),f1(x),f2(x)在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“伴随函数”.已知函数f1(x)=(a-
| 1 |
| 2 |
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:
分析:(Ⅰ)当a=2时,求函数的导数,利用函数的单调性和导数之间的关系,即可求f(x)在区间[e,e2]上的最大值和最小值;
(Ⅱ)构造函数p(x)=f(x)-f2(x)和h(x)=f1(x)-f(x),将不等式转化为恒成立问题,利用导数和函数最值之间的关系,即可求出a的取值范围.
(Ⅱ)构造函数p(x)=f(x)-f2(x)和h(x)=f1(x)-f(x),将不等式转化为恒成立问题,利用导数和函数最值之间的关系,即可求出a的取值范围.
解答:
解:(Ⅰ)当a=2时,f(x)=2x2+lnx,
则f'(x)=4x+
=
,
当x∈[e,e2]时,f'(x)>0,
即此时函数f(x)单调递增,
∴f(x)的最大值为f(e2)=2e4+lne2=2+2e4,
最小值为f(e)=2e2+lne=1+2e2.
(Ⅱ)若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,
则f1(x)<f(x)<f2(x),
令p(x)=f(x)-f2(x)=(a-
)x2-2ax+lnx<0在(1,+∞)上恒成立,
h(x)=f1(x)-f(x)=-
x2+2ax-a2lnx<0在(1,+∞)上恒成立,
∵p'(x)=(2a-1)x-2a+
=
=
,
①若a>
,由p'(x)=0得x1=1或x2=
,
当x2>x1=1,即
<a<1时,在(x2,+∞)上,有p'(x)>0,此时函数单调递增,并且在该区间上有p(x)∈(p(x2),+∞),不合题意.
当x2<x1=1,即a≥1时,同理可知在区间(1,+∞)上,有p(x)∈(p(1),+∞),不合题意.
②若a≤
,则有2a-1≤0,此时在区间(1,+∞)上,有p'(x)<0,此时函数p(x)单调递减,
要使p(x)<0恒成立,只需要满足p(1)=-a-
≤0,即a≥-
即可,
此时-
≤a≤
.
又h′(x)=-x+2a-
=
=
<0,
则h(x)在(1,+∞)上为减函数,
则h(x)<h(1)=
+2a≤0,
∴a≤
,
综上-
≤a≤
,
即a的取值范围是[-
,
].
则f'(x)=4x+
| 1 |
| x |
| 4x2+1 |
| x |
当x∈[e,e2]时,f'(x)>0,
即此时函数f(x)单调递增,
∴f(x)的最大值为f(e2)=2e4+lne2=2+2e4,
最小值为f(e)=2e2+lne=1+2e2.
(Ⅱ)若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,
则f1(x)<f(x)<f2(x),
令p(x)=f(x)-f2(x)=(a-
| 1 |
| 2 |
h(x)=f1(x)-f(x)=-
| 1 |
| 2 |
∵p'(x)=(2a-1)x-2a+
| 1 |
| x |
| (2a-1)x2-2ax+1 |
| x |
| (x-1)[(2a-1)x-1] |
| x |
①若a>
| 1 |
| 2 |
| 1 |
| 2a-1 |
当x2>x1=1,即
| 1 |
| 2 |
当x2<x1=1,即a≥1时,同理可知在区间(1,+∞)上,有p(x)∈(p(1),+∞),不合题意.
②若a≤
| 1 |
| 2 |
要使p(x)<0恒成立,只需要满足p(1)=-a-
| 1 |
| 2 |
| 1 |
| 2 |
此时-
| 1 |
| 2 |
| 1 |
| 2 |
又h′(x)=-x+2a-
| a2 |
| x |
| -x2+2ax-a2 |
| x |
| -(x-a)2 |
| x |
则h(x)在(1,+∞)上为减函数,
则h(x)<h(1)=
| 1 |
| 2 |
∴a≤
| 1 |
| 4 |
综上-
| 1 |
| 2 |
| 1 |
| 4 |
即a的取值范围是[-
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题主要考查函数最值的计算,利用导数是解决本题的关键,综合性较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设A是半径为1的圆周上一定点,P是圆周上一动点,则弦PA<1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知菱形ABCD的边长为4,∠ABC=150°,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( )
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
 如图,F是椭圆
如图,F是椭圆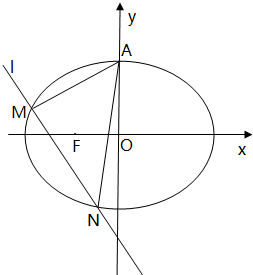 已知椭圆C:
已知椭圆C: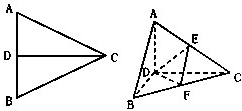 CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.