题目内容
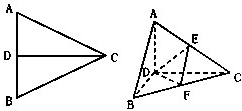 CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.(Ⅰ)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)若AC=2,求棱锥E-DFC的体积;
(Ⅲ)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出
| AP |
| AC |
考点:与二面角有关的立体几何综合题,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)AB∥平面DEF.在△ABC中,E,F分别是AC和BC的中点,由此能证明AB∥平面DEF.
(Ⅱ)由已知条件推导出AD⊥平面BCD,取CD的中点M,能求出EM⊥平面BCD,EM=1,由此能求出棱锥E-DFC的体积.
(Ⅲ)在线段AC上存在点P,使BP⊥DF.在AC上取点P,使AP=
,过点P作PQ⊥CD于Q,由此能求出
=
.
(Ⅱ)由已知条件推导出AD⊥平面BCD,取CD的中点M,能求出EM⊥平面BCD,EM=1,由此能求出棱锥E-DFC的体积.
(Ⅲ)在线段AC上存在点P,使BP⊥DF.在AC上取点P,使AP=
| AC |
| 3 |
| AP |
| AC |
| 1 |
| 3 |
解答:
解:(Ⅰ)AB∥平面DEF.理由如下:
∵CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,
现将△ABC沿CD翻折成直二面角A-DC-B,
如图,在△ABC中,E,F分别是AC和BC的中点,∴EF∥AB,
∵AB不包含于平面DEF,EF?平面DEF,
∴AB∥平面DEF.
(Ⅱ)∵CD是正△ABC的边AB上的高,
∴AD⊥CD,BD⊥CD,
将△ABC沿CD翻折成直二面角A-DC-B,
依然满足AD⊥CD,BD⊥CD,
∴CD⊥平面ABD,
在直二面角A-DC-B中,
∵AD⊥CD,∴AD⊥平面BCD,
∵BD?平面BCD,∴AD⊥BD,
取CD的中点M,则EM∥AD,∴EM⊥平面BCD,
∵AC=2,△ABC是正三角形,∴BC=2,AD=BD=1,
∴EM=
AD=
,S△DFC=
×1×
=
,
∴VE-DFC=
×EM×S△DFC=
•
•
=
.
(Ⅲ)在线段AC上存在点P,使BP⊥DF.
证明:在AC上取点P,使AP=
,
过点P作PQ⊥CD于Q,
连结DF,BQ,交于点O,
在Rt△BCD中,∵BD=BF=DF=1,∴∠BDO=60°,
∵DQ=
CD=
,∴tan∠DBO=
=
,
∴∠DBO=30°,∴∠BOD=90°,∴DF⊥BQ,
∵DF⊥CQ,BQ∩CQ=Q,
∴DF⊥平面BPQ,∴BP⊥DF,
此时AP=
AC,∴
=
.
∵CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,
现将△ABC沿CD翻折成直二面角A-DC-B,
如图,在△ABC中,E,F分别是AC和BC的中点,∴EF∥AB,
∵AB不包含于平面DEF,EF?平面DEF,
∴AB∥平面DEF.
(Ⅱ)∵CD是正△ABC的边AB上的高,
∴AD⊥CD,BD⊥CD,
将△ABC沿CD翻折成直二面角A-DC-B,

依然满足AD⊥CD,BD⊥CD,
∴CD⊥平面ABD,
在直二面角A-DC-B中,
∵AD⊥CD,∴AD⊥平面BCD,
∵BD?平面BCD,∴AD⊥BD,
取CD的中点M,则EM∥AD,∴EM⊥平面BCD,
∵AC=2,△ABC是正三角形,∴BC=2,AD=BD=1,
∴EM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| CD |
| 2 |
| 1 |
| 4 |
| 3 |
∴VE-DFC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| ||
| 24 |
(Ⅲ)在线段AC上存在点P,使BP⊥DF.
证明:在AC上取点P,使AP=
| AC |
| 3 |
过点P作PQ⊥CD于Q,
连结DF,BQ,交于点O,
在Rt△BCD中,∵BD=BF=DF=1,∴∠BDO=60°,
∵DQ=
| 1 |
| 3 |
| ||
| 3 |
| DQ |
| BD |
| ||
| 3 |
∴∠DBO=30°,∴∠BOD=90°,∴DF⊥BQ,
∵DF⊥CQ,BQ∩CQ=Q,
∴DF⊥平面BPQ,∴BP⊥DF,
此时AP=
| 1 |
| 3 |
| AP |
| AC |
| 1 |
| 3 |
点评:本题考查直线与平面的位置关系的判断与证明,考查棱锥体积的求法,考查满足条件的点提否存在的判断,解题时要注意空间思维能力的培养.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知函数f(x)的定义域为(-∞,+∞),如果f(x+2014)=
那么f(2014+
)•f(-7986)=( )
|
| π |
| 4 |
| A、2014 | ||
| B、4 | ||
C、
| ||
D、
|