将一个三角形木块水平放置.其平面直观图是如图所示的腰长为1的等腰直角三角形.则这个木块的面积是( )A．$\frac{1}{2}$B．$\sqrt{2}$C．2$\sqrt{2}$D．4$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

12．

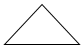将一个三角形木块水平放置，其平面直观图是如图所示的腰长为1的等腰直角三角形，则这个木块的面积是（　　）

A．

$\frac{1}{2}$

B．

$\sqrt{2}$

C．

2$\sqrt{2}$

D．

4$\sqrt{2}$

分析先计算直观图的面积，进而根据S_原图=2$\sqrt{2}$S_直观图，得到答案．

解答解：将一个三角形木块水平放置，其平面直观图是如图所示的腰长为1的等腰直角三角形，
故直观图的面积：S_直观图=$\frac{1}{2}$，
∴原图的面积：S_原图=2$\sqrt{2}$S_直观图=$\sqrt{2}$，
故选：B．

点评本题考查的知识点是平面图形的直观图，熟练掌握S_原图=2$\sqrt{2}$S_直观图，是解答的关键．

练习册系列答案

3．观察下列数列当n→∞时有无极限：
（1）1，-1，1，…，（-1）^n-1，…；
（2）$\frac{1}{2}$，$\frac{1}{4}$，$\frac{1}{8}$，…，$\frac{1}{{2}^{n}}$，…；
（3）$\frac{1}{2}$，$\frac{2}{3}$，$\frac{3}{4}$，…，$\frac{n}{n+1}$，…；
（4）1，3，5，…，2n-1，…

20．若函数f（x）=3sin（ωx+φ）对任意实数x都有f（$\frac{π}{3}$+x）=f（$\frac{π}{3}$-x）恒成立，则f（$\frac{π}{3}$）等于（　　）

7．对于函数f（x），若存在x₀∈Z，满足|f（x₀）|≤$\frac{1}{4}$，则称x₀为函数f（x）的一个“近零点”．已知函数f（x）=ax²+bx+c（a＞0）有四个不同的“近零点”，则a的最大值为（　　）

17．如图，在△ABC中，$\overrightarrow{BD}=2\overrightarrow{DC}$，若$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}=\overrightarrow b$，则$\overrightarrow{AD}$=（　　）

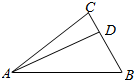
A．

$\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$

B．

$\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$

C．

$\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$

D．

$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$

4．在平面直角坐标系xOy中，曲线C₁的参数方程为：$\left\{\begin{array}{l}{x=cosθ}\\{y=3sinθ}\end{array}\right.$（θ为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，得曲线C₂的极坐标方程为ρ-6sinθ+8cosθ=0（ρ≥0）．
（1）求曲线C₁的普通方程和曲线C₂的直角坐标方程：
（2）直钱l：$\left\{\begin{array}{l}{x=2+t}\\{y=-\frac{3}{2}+λt}\end{array}\right.$（t为参数）过曲线C₁与y轴负半轴的交点，求直线l平行且与曲线C₂相切的直线方程．

1．若函数f（x）=$\frac{x-4}{m{x}^{2}+4mx+3}$的定义域为R，则实数m的取值范围是（　　）

2．已知命题p：?x∈[l，2]，m≤x²，命题q：?x∈R，x²+mx+l＞0
（Ⅰ）写出“￢p命题；
（Ⅱ）若命题p∧q为真命题，求实数m的取值范围．

试题分类