题目内容
3.观察下列数列当n→∞时有无极限:(1)1,-1,1,…,(-1)n-1,…;
(2)$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$,…;
(3)$\frac{1}{2}$,$\frac{2}{3}$,$\frac{3}{4}$,…,$\frac{n}{n+1}$,…;
(4)1,3,5,…,2n-1,…
分析 (1)讨论n为奇数或偶数,即可判断是否存在极限;
(2)当n→∞时,$\frac{1}{{2}^{n}}$→0,可得极限;
(3)运用当n→∞时,$\frac{1}{n}$→0,即可得到所求极限;
(4)当n→∞时,an=2n-1→+∞,即可判断是否存在极限.
解答 解:(1)由an=(-1)n-1,可得n为偶数时,an=1;n为奇数时,an=-1.则当n→∞时an无极限;
(2)当n→∞时,$\frac{1}{{2}^{n}}$→0,可得极限为0;
(3)当n→∞时,$\frac{1}{n}$→0,可得$\frac{n}{n+1}$=$\frac{1}{1+\frac{1}{n}}$→1,
则所求极限为1;
(4)当n→∞时,an=2n-1→+∞,
可得an无极限.
点评 本题考查数列极限的求法,注意运用数列极限的公式,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.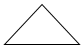 将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )
将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )
 将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )
将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
13.在△ABC中,已知三条边上的高线长分别为$\frac{1}{3}$,$\frac{1}{5}$,$\frac{1}{7}$,则△ABC的最大内角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
 如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.
如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.