题目内容
7.对于函数f(x),若存在x0∈Z,满足|f(x0)|≤$\frac{1}{4}$,则称x0为函数f(x)的一个“近零点”.已知函数f(x)=ax2+bx+c(a>0)有四个不同的“近零点”,则a的最大值为( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 易知a不变时,函数f(x)的图象的形状不变,且四个不同的“近零点”的最小间距为3,对称轴在区间中间时可取到a的最大值,从而解得.
解答 解:∵a不变时,函数f(x)的图象的形状不变;
∴记f(x)=a(x-k)2+h,
四个不同的“近零点”的最小间距为3,
故易知对称轴在区间中间时可取到a的最大值,
故不妨记f(x)=a(x-$\frac{1}{2}$)2+h,
故f(-1)-f(0)≤$\frac{1}{4}$×2,
即$\frac{9}{4}$a+h-($\frac{1}{4}$a+h)≤$\frac{1}{2}$,
故a≤$\frac{1}{4}$,
故选D.
点评 本题考查了学生对新定义的接受能力及二次函数的图象的形状应用.

练习册系列答案
相关题目
12.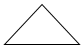 将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )
将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )
 将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )
将一个三角形木块水平放置,其平面直观图是如图所示的腰长为1的等腰直角三角形,则这个木块的面积是( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
16.已知直线x-ay=4在y轴上的截距是2,则a等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
17.sin347°cos148°+sin77°cos58°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
 如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.
如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.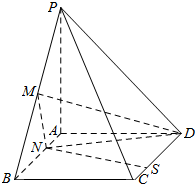 已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.
已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.