题目内容
复数z=i（i+1），在复平面内，与复数z对应的点Z所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用多项式的乘法运算法则求出复数z，得到点的坐标，判断所在象限即可．
解答：
解：复数z=i（i+1）=-1+i，
在复平面内，与复数z对应的点Z（-1，1）所在的象限是第二象限．
故选：B．
在复平面内，与复数z对应的点Z（-1，1）所在的象限是第二象限．
故选：B．
点评：本题考查复数的代数形式的混合运算，复数对应点的坐标所在象限，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
设一组数据31，37，33，a，35的平均数是34，则这组数据的方差是（ ）
| A、2.5 | B、3 | C、3.5 | D、4 |
若x，y满足约束条件
，则
的最小值为（ ）
|
| x |
| y |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
设函数f（x）的定义域为D，若存在非零实数t使得对于任意x∈M（M⊆D），有x+t∈D，且f（x+t）≥f（x），则称f（x）为M上的“t高调函数”．如果定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x-a2|-a2，且f（x）为R上的“4高调函数”，那么实数a的取值范围是（ ）
A、[-
| ||||||||
| B、[-1，1] | ||||||||
C、[-1，
| ||||||||
D、[-
|
下列函数中既是奇函数，又在区间（0，+∞）上单调递减的函数是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
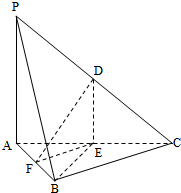如图，在三棱锥P-ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：
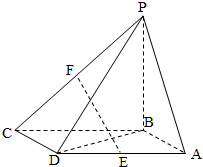如图，四棱锥P-ABCD的底面ABCD是平行四边形，BA=BD=