题目内容
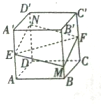 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题:①平面MENF⊥平面BDD′B′;
②平面MENF的为矩形;
③当M为BB′的中点时,MENF的面积最小;
④四棱锥C′-MENF的体积为常数;
以上命题中正确命题的序号为
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:结合直线、平面的垂直和平行的条件进行逐个验证即可.
解答:
解:对于①:显然,EF⊥BD,又EF⊥DD′,
∴EF⊥平面BDD′B′,
∴平面MENF⊥平面BDD′B′;
∴①正确;
对于②:∵平面ADD′A′∥平面BCC′B′,
∴EN∥MF,且EN=MF,
∴四边形EMFN为平行四边形,
∴四边形MENF为平行四边形,
故②错误;
对于③:MENF的面积=EF×MN,
当M为BB′的中点时,MN最短,此时面积最小.
故③正确;
对于④:连结C′E,C′M,C′N,则四棱锥则分割为两个小三棱锥,
它们以C′EF为底,以M,N分别为顶点的两个小棱锥.
因为三角形C′EF的面积是个常数.M,N到平面C'EF的距离是个常数,
所以四棱锥C'-MENF的体积V为常函数,所以④正确.
综上,正确的有①③④.
故答案为:①③④.

∴EF⊥平面BDD′B′,
∴平面MENF⊥平面BDD′B′;
∴①正确;
对于②:∵平面ADD′A′∥平面BCC′B′,
∴EN∥MF,且EN=MF,
∴四边形EMFN为平行四边形,
∴四边形MENF为平行四边形,
故②错误;
对于③:MENF的面积=EF×MN,
当M为BB′的中点时,MN最短,此时面积最小.
故③正确;
对于④:连结C′E,C′M,C′N,则四棱锥则分割为两个小三棱锥,
它们以C′EF为底,以M,N分别为顶点的两个小棱锥.
因为三角形C′EF的面积是个常数.M,N到平面C'EF的距离是个常数,
所以四棱锥C'-MENF的体积V为常函数,所以④正确.
综上,正确的有①③④.
故答案为:①③④.
点评:本题重点考查了空间中平行和垂直关系的判断和性质等知识,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
已知全集U=R,集合M={x|-2≤x-1≤2},N={x|x=2k-1,k=1,2,…},则M∩N等于( )
| A、{1} |
| B、{1,3} |
| C、{-1,1,3} |
| D、{-1,0,1,3} |
曲线y=e
x在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| A、e2 | ||
| B、2e2 | ||
| C、4e2 | ||
D、
|
下列式子正确的是( )
A、(
| ||||||||||||
B、
| ||||||||||||
C、|
| ||||||||||||
D、
|
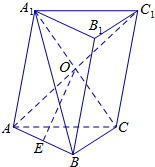 如图,斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是AB的中点.求证:
如图,斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是AB的中点.求证: