题目内容
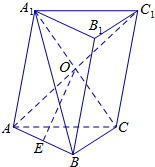如图，斜三棱柱ABC-A1B1C1中，侧面AA1C1C是菱形，AC1与A1C交于点O，E是AB的中点．求证：（1）OE∥平面BCC1B1；
（2）若AC1⊥A1B，求证：AC1⊥BC．
考点：直线与平面平行的判定,空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：（1）首先通过连接对角线得到中点，进一步利用中位线，得到线线平行，进一步利用线面平行的判定定理，得到结论．
（2）利用菱形的对角线互相垂直，进一步利用线面垂直的判定定理，得到线面垂直，最后转化成线线垂直．
（2）利用菱形的对角线互相垂直，进一步利用线面垂直的判定定理，得到线面垂直，最后转化成线线垂直．
解答：
证明：（1）连结BC1．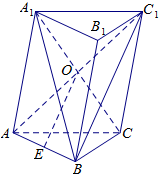
∵侧面AA1C1C是菱形，AC1与A1C交于点O
∴O为AC1的中点
∵E是AB的中点
∴OE∥BC1；
∵OE?平面BCC1B1，BC1?平面BCC1B1
∴OE∥平面BCC1B1
（2）∵侧面AA1C1C是菱形
∴AC1⊥A1C
∵AC1⊥A1B，A1C∩A1B=A1，A1C?平面A1BC，A1B?平面A1BC
∴AC1⊥平面A1BC
∵BC?平面A1BC
∴AC1⊥BC．
∵侧面AA1C1C是菱形，AC1与A1C交于点O
∴O为AC1的中点
∵E是AB的中点
∴OE∥BC1；
∵OE?平面BCC1B1，BC1?平面BCC1B1
∴OE∥平面BCC1B1
（2）∵侧面AA1C1C是菱形
∴AC1⊥A1C
∵AC1⊥A1B，A1C∩A1B=A1，A1C?平面A1BC，A1B?平面A1BC
∴AC1⊥平面A1BC
∵BC?平面A1BC
∴AC1⊥BC．
点评：本题考查的知识要点：线面平行的判定定理，线面垂直的判定定理和性质定理，属于基础题型．
练习册系列答案
相关题目
已知函数f（x）=
，（其中a＞1），则f[f（a2）]=（ ）
|
| A、0 | B、1 |
| C、2 | D、loga2 |
已知全集U={0，1，2}，且∁UA={2}，则集合A等于（ ）
| A、{0} | B、{0，1} |
| C、{1} | D、∅ |
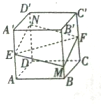如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′交于M、N，给出以下四个命题：
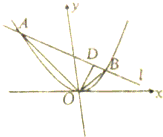如图，已知直线l与顶点在原点O，焦点在y轴的正半轴上的抛物线C相交于A，B两点，且OA⊥OB，垂足D的坐标为（1，2）．