题目内容
已知函数f(x)=x2-2ax+3,g(x)=mx+5-2m.
(Ⅰ)若函数F(x)=f(3x),x∈[-1,1],F(x)的最小值为h(a),求h(a)的解析式;
(Ⅱ)若x∈[1,4],当a=2时f(x)的值域为A,g(x)的值域为B,A∪B=B,求m的取值范围.
(Ⅰ)若函数F(x)=f(3x),x∈[-1,1],F(x)的最小值为h(a),求h(a)的解析式;
(Ⅱ)若x∈[1,4],当a=2时f(x)的值域为A,g(x)的值域为B,A∪B=B,求m的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)换元法转化为二次函数求解,F(x)=y=t2-2at+3=(t-a)2+3-a2,则对称轴为t=a,根据对称轴与区间 的关系讨论①当a≤
时,t=
时,F(x)min=h(a)=
-
,②当
<a<3时,t=a时,F(x)min=h(a)=3-a2,③当a≥3时,t=3时,F(x)min=h(a)=12-6a.
(Ⅱ)分类讨论求解即可①当m=0时,g(x)=5,为常数,不符合题意;②当m>0时,B=[5-m,5+2m],需
,解得m≥6,
③当m<0时,B=[5+2m,5-m],需
,解得m≤-3.
| 1 |
| 3 |
| 1 |
| 3 |
| 28 |
| 9 |
| 2a |
| 3 |
| 1 |
| 3 |
(Ⅱ)分类讨论求解即可①当m=0时,g(x)=5,为常数,不符合题意;②当m>0时,B=[5-m,5+2m],需
|
③当m<0时,B=[5+2m,5-m],需
|
解答:
解:(Ⅰ)设t=3x,∵x∈[-1,1],∴t∈[
,3],
令F(x)=y=t2-2at+3=(t-a)2+3-a2,则对称轴为t=a,
①当a≤
时,t=
时,F(x)min=h(a)=
-
,
②当
<a<3时,t=a时,F(x)min=h(a)=3-a2,
③当a≥3时,t=3时,F(x)min=h(a)=12-6a.
综上:h(a)=
,
(Ⅱ)当a=2时,f(x)=x2-4x+3=(x-2)2-1
∵x∈[1,4],∴f(x)的值域A=[-1,3],
∵A∪B=B,∴A⊆B,下面求g(x)的值域B
①当m=0时,g(x)=5,为常数,不符合题意;
②当m>0时,B=[5-m,5+2m],∵A⊆B,
需
,解得m≥6,
③当m<0时,B=[5+2m,5-m],∵A⊆B,
需
,解得m≤-3.
综上:m≥6或m≤-3.
| 1 |
| 3 |
令F(x)=y=t2-2at+3=(t-a)2+3-a2,则对称轴为t=a,
①当a≤
| 1 |
| 3 |
| 1 |
| 3 |
| 28 |
| 9 |
| 2a |
| 3 |
②当
| 1 |
| 3 |
③当a≥3时,t=3时,F(x)min=h(a)=12-6a.
综上:h(a)=
|
(Ⅱ)当a=2时,f(x)=x2-4x+3=(x-2)2-1
∵x∈[1,4],∴f(x)的值域A=[-1,3],
∵A∪B=B,∴A⊆B,下面求g(x)的值域B
①当m=0时,g(x)=5,为常数,不符合题意;
②当m>0时,B=[5-m,5+2m],∵A⊆B,
需
|
③当m<0时,B=[5+2m,5-m],∵A⊆B,
需
|
综上:m≥6或m≤-3.
点评:本题考查了函数的性质,分类讨论的思想,不等式的运用,属于综合题,但是难度不大,关键是确定分类的标准.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
y=ax2+bx+c(a≠0)的图象如图所示,则点M(a,bc)在( )
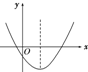

| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
非零向量
,
满足
•
-2
2
2=0,|
|+|
|=1,则
与
的夹角的最小值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=0,且AB⊥CD,SO=OB=2,P为SB的中点.异面直线SA与PD所成角的正切值为( )
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=0,且AB⊥CD,SO=OB=2,P为SB的中点.异面直线SA与PD所成角的正切值为( )