题目内容
已知直线l1:ax-2y-2a+4=0,l2:2x+a2y-2a2-4=0,其中0<a<2,当l1,l2与两坐标轴围成的四边形面积最小时,求l1与l2的方程.
考点:直线的一般式方程
专题:直线与圆
分析:对于直线l1:ax-2y-2a+4=0,分别令x=0,y=0 可得与坐标轴的交点A,B.对于l2:2x+a2y-2a2-4=0,分别令x=0,y=0 可得与坐标轴的交点C,D.可得l1,l2与两坐标轴围成的四边形面积S=
|AC||BD|,再利用基本不等式的性质即可得出.
| 1 |
| 2 |
解答:
解:∵0<a<2,对于直线l1:ax-2y-2a+4=0,分别令x=0,y=0 可得与坐标轴的交点A(0,2-a),B(
,0).
对于l2:2x+a2y-2a2-4=0,分别令x=0,y=0 可得与坐标轴的交点,C(0,2+
),D(a2+2,0).
∴l1,l2与两坐标轴围成的四边形面积S=
|AC||BD|=
|(a+
)(a2+
)|=
(a3+
+8)≥
(2
+8)=8,当且仅当a=
时取等号.
∴l1与l2的方程分别为:
x-2y-2
+4=0;2x+
y-2
-4=0.
| 2a-4 |
| a |
对于l2:2x+a2y-2a2-4=0,分别令x=0,y=0 可得与坐标轴的交点,C(0,2+
| 4 |
| a2 |
∴l1,l2与两坐标轴围成的四边形面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| a2 |
| 4 |
| a |
| 1 |
| 2 |
| 16 |
| a3 |
| 1 |
| 2 |
a3•
|
| 3 | 4 |
∴l1与l2的方程分别为:
| 3 | 4 |
| 3 | 4 |
| 3 | 16 |
| 3 | 16 |
点评:本题考查了直线与坐标轴的交点、四边形的面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
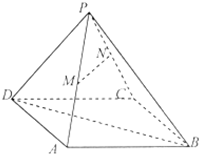 如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2
如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2