题目内容
 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=0,且AB⊥CD,SO=OB=2,P为SB的中点.异面直线SA与PD所成角的正切值为( )
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=0,且AB⊥CD,SO=OB=2,P为SB的中点.异面直线SA与PD所成角的正切值为( )| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:异面直线及其所成的角
专题:空间角
分析:连结PO,则PO∥SA,从而∠DPO为异面直线SA与PD所成角,由此能求出异面直线SA与PD所成角的正切值.
解答:
解:连结PO,
∵P、O分别为SB、AB的中点,
∴PO∥SA,
∴∠DPO为异面直线SA与PD所成角,
∵CD⊥AB,CD⊥SO,AB∩SO=O,
∴CD⊥平面SOB,
∴OD⊥PO,
在Rt△DOP中,OD=2,OP=
SB=
,
∴tan∠DPO=
=
=
,
∴异面直线SA与PD所成角的正切值为
.
故选:B.

∵P、O分别为SB、AB的中点,
∴PO∥SA,
∴∠DPO为异面直线SA与PD所成角,
∵CD⊥AB,CD⊥SO,AB∩SO=O,
∴CD⊥平面SOB,
∴OD⊥PO,
在Rt△DOP中,OD=2,OP=
| 1 |
| 2 |
| 2 |
∴tan∠DPO=
| OD |
| OP |
| 2 | ||
|
| 2 |
∴异面直线SA与PD所成角的正切值为
| 2 |
故选:B.
点评:本题考查异面直线SA与PD所成角的正切值的求法,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知向量
=(2cosφ,2sinφ),φ∈(90°,180°),
=(1,1),则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、φ | B、φ-45° |
| C、135°-φ | D、45°-φ |
已知点A(1,5),B(3,9),O为坐标原点,若点C满足
=α
+β
,其中α,β∈R,且α+β=1,则点C的轨迹方程为( )
| OC |
| OA |
| OB |
| A、2x+y-7=0 |
| B、2x-y+3=0 |
| C、x-2y+9=0 |
| D、x+2y-11=0 |
数列前n项和为n3,且前n个偶数项的和为n2(4n+3),则前n个奇数项的和为( )
| A、-3n2(n+1) | ||
| B、n2(4n-3) | ||
| C、-3n2 | ||
D、
|
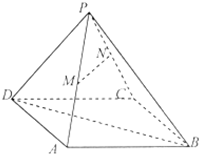 如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2
如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2