题目内容
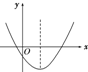
y=ax2+bx+c(a≠0)的图象如图所示,则点M(a,bc)在( )

| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:二次函数的性质
专题:函数的性质及应用
分析:根据已知中y=ax2+bx+c(a≠0)的图象,分析a,b,c的符号,进而可得M点的位置.
解答:
解:∵y=ax2+bx+c(a≠0)的图象开口方向朝上,
∴a>0,
又由对称轴在y轴右侧,故-
>0,
∴b<0,
当x=0时,图象与y轴交点在y轴负半轴上,
∴c<0,
故bc>0,
即点M(a,bc)在第一象限,
故选:A.
∴a>0,
又由对称轴在y轴右侧,故-
| b |
| 2a |
∴b<0,
当x=0时,图象与y轴交点在y轴负半轴上,
∴c<0,
故bc>0,
即点M(a,bc)在第一象限,
故选:A.
点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
已知点A(1,5),B(3,9),O为坐标原点,若点C满足
=α
+β
,其中α,β∈R,且α+β=1,则点C的轨迹方程为( )
| OC |
| OA |
| OB |
| A、2x+y-7=0 |
| B、2x-y+3=0 |
| C、x-2y+9=0 |
| D、x+2y-11=0 |
数列前n项和为n3,且前n个偶数项的和为n2(4n+3),则前n个奇数项的和为( )
| A、-3n2(n+1) | ||
| B、n2(4n-3) | ||
| C、-3n2 | ||
D、
|