题目内容
 如图,摩天轮上一点P在t时刻距离地面高度满足y=Asin(ωt+φ)+b,φ∈
如图,摩天轮上一点P在t时刻距离地面高度满足y=Asin(ωt+φ)+b,φ∈[-π,π],已知某摩天轮的半径为50米,点O距地面的高度为60米,摩天轮
做匀速转动,每3分钟转一圈,点P的起始位置在摩天轮的最低点处.
(1)根据条件写出y(米)关于t(分钟)的解析式;
(2)在摩天轮转动的一圈内,有多长时间点P距离地面超过85米?
考点:在实际问题中建立三角函数模型
专题:计算题,应用题,三角函数的图像与性质
分析:(1)由题意,A=50,b=60,T=3;从而可得y=50sin(
t+φ)+60;再代入初相即可;
(2)在第一个3分钟内求即可,令50sin(
t-
)+60>85解得.
| 2π |
| 3 |
(2)在第一个3分钟内求即可,令50sin(
| 2π |
| 3 |
| π |
| 2 |
解答:
解:(1)由题意,
A=50,b=60,T=3;
故ω=
,
故y=50sin(
t+φ)+60;
则由50sinφ+60=10及φ∈[-π,π]得,
φ=-
;
故y50sin(
t-
)+60;
(2)在第一个3分钟内求即可,
令50sin(
t-
)+60>85;
则sin(
t-
)>
;
故
<
t-
<
,
解得,1<t<2;
故在摩天轮转动的一圈内,有1分钟时间点P距离地面超过85米.
A=50,b=60,T=3;
故ω=
| 2π |
| 3 |
故y=50sin(
| 2π |
| 3 |
则由50sinφ+60=10及φ∈[-π,π]得,
φ=-
| π |
| 2 |
故y50sin(
| 2π |
| 3 |
| π |
| 2 |
(2)在第一个3分钟内求即可,
令50sin(
| 2π |
| 3 |
| π |
| 2 |
则sin(
| 2π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
故
| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
解得,1<t<2;
故在摩天轮转动的一圈内,有1分钟时间点P距离地面超过85米.
点评:本题考查了三角函数在实际问题中的应用,属于基础题.

练习册系列答案
相关题目
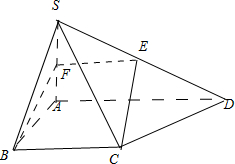 在四棱锥S-ABCD中,底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA=
在四棱锥S-ABCD中,底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA=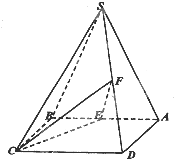 如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=
如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=