Question

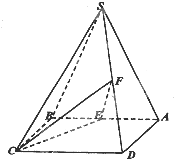如图，四棱锥S-ABCD的底面ABCD是正方形，侧面SAB是等腰三角形且垂直于底面，SA=SB=

5

，AB=2，E、F分别是AB、SD的中点．
（1）求证：EF∥平面SBC：
（2）求二面角F-CE-A的大小．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（1）以E为原点，在平面ABCD内过E垂直于AB的直线为x轴，以EA为y轴，ES为z轴，建立空间直角坐标系，利用向量法能证明EF∥平面SBC．
（2）求出平面CEF的法向量和平面ACE的法向量，利用向量法能求出二面角F-CE-A的余弦值．

解答： （1）证明：以E为原点，在平面ABCD内过E垂直于AB的直线为x轴，
以EA为y轴，ES为z轴，建立空间直角坐标系，
由已知得E（0，0，0），D（2，1，0），
S（0，0，2），F（1，

1

2

，1），
B（0，-1，0），C（2，-1，0），

SB

=（0，-1，-2），

SC

=（2，-1，-2），
设平面SBC的法向量

n

=（x，y，z），
则

n • SB =-y-2z=0 n • SC =2x-y-2z=0

，取y=2，得

n

=（0，2，-1），

EF

=（1，

1

2

，1），
∵

EF

•

n

=0，EF在平面SBC外，
∴EF∥平面SBC．
（2）解：设

m

=（a，b，c）为平面CEF的法向量，
∵

EC

=(2，-1，0)，

EF

=(1，

1

2

，1)，
∴

m • EC =2a-b=0 m • EF =a+ 1 2 b+c=0

，取a=1，得

m

=（1，2，-2），
又

p

=（0，0，1）是平面ACE的法向量，
设二面角F-CE-A的平面角为θ，
cosθ=|cos＜

m

，

n

＞|=|

-2

9

|=

2

3

，
∴二面角F-CE-A的余弦值为

2

3

．

点评：本题考查直线与平面平行的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．