题目内容
3.已知函数$f(x)=xlnx,g(x)=\frac{{a{x^2}}}{2}$.(1)求函数f(x)在x=e处的切线方程;
(2)若至少存在一个x0∈[1,e]使f(x0)<g(x0)成立,求实数a的取值范围;
(3)设k∈Z且f(x)>(k-3)x-k+2在x>1时恒成立,求整数k的最大值.
分析 (1)求出原函数的导函数,得到f′(e),再求出f(e),达人直线方程的点斜式得答案;
(2)由存在一个x0∈[1,e]使f(x0)<g(x0)成立,得x0lnx0<$\frac{a{{x}_{0}}^{2}}{2}$,分离参数a,令h(x)=$\frac{2lnx}{x}$,利用导数求其最小值得答案;
(3)由题意得:xlnx>(k-3)x-k+2在x>1时恒成立,即k<$\frac{xlnx+3x-2}{x-1}$.构造函数F(x)=$\frac{xlnx+3x-2}{x-1}$,得F′(x)=$\frac{x-lnx-2}{(x-1)^{2}}$.令m(x)=x-lnx-2,则m′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$>0在x>1时恒成立.然后利用函数F(x)的单调性求其最小值$F(x)_{min}=F(b)=\frac{blnb+3b-2}{b-1}$=$\frac{b(b-2)+3b-2}{b-1}=b+2$∈(5,6).从而可得整数k的最大值.
解答 解:(1)f′(x)=lnx+1,∴f′(e)=2,由f(e)=e,
∴函数f(x)在x=e处的切线方程为y-e=2(x-e),
即2x-y-e=0;
(2)若存在一个x0∈[1,e]使f(x0)<g(x0)成立,
即x0lnx0<$\frac{a{{x}_{0}}^{2}}{2}$,则a>$\frac{2ln{x}_{0}}{{x}_{0}}$.
令h(x)=$\frac{2lnx}{x}$,当x∈[1,e)时,h′(x)=$\frac{2(1-lnx)}{{x}^{2}}$>0恒成立.
因此,h(x)=$\frac{2lnx}{x}$在[1,e]上单调递增,故当x=1时,h(x)min=0.
即实数a的取值范围为(0,+∞);
(3)由题意得:xlnx>(k-3)x-k+2在x>1时恒成立,即k<$\frac{xlnx+3x-2}{x-1}$.
令F(x)=$\frac{xlnx+3x-2}{x-1}$,则F′(x)=$\frac{x-lnx-2}{(x-1)^{2}}$.
令m(x)=x-lnx-2,则m′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$>0在x>1时恒成立.
∴m(x)在(1,+∞)上单调递增,且m(3)=1-ln3<0,m(4)=2-ln4>0.
∴在(1,+∞)上存在唯一实数b(b∈(3,4)),使m(x)=0,即m(b)=0.
当1<x<b时,m(x)<0,即F′(x)<0,当x>b,m(x)>0,即F′(x)>0.
∴F(x)在(1,b)上单调递减,在(b,+∞)上单调递增.
∴$F(x)_{min}=F(b)=\frac{blnb+3b-2}{b-1}$=$\frac{b(b-2)+3b-2}{b-1}=b+2$∈(5,6).
故k<b+2,又k∈Z,∴整数k的最大值为5.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查利用导数求函数在闭区间上的最值,考查逻辑思维能力与推理运算能力,难度较大.

| A. | (-1,0] | B. | [0,4) | C. | (0,4] | D. | [-1,0) |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 |
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(万件) | 11 | 10 | 8 | 6 | 5 |
| A. | 14.2元 | B. | 10.8元 | C. | 14.8元 | D. | 10.2元 |
| A. | $\frac{13}{5}$ | B. | $-\frac{13}{5}$ | C. | $\frac{{13\sqrt{53}}}{53}$ | D. | $-\frac{{13\sqrt{53}}}{53}$ |
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形但不是等腰三角形 | D. | 等腰三角形但不是直角三角形 |
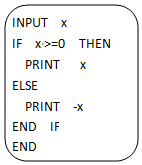 当输入的x 值为-5时,如图的程序运行的结果等于5.
当输入的x 值为-5时,如图的程序运行的结果等于5.