题目内容
12.椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F1(-2,0),离心率e=$\frac{1}{2}$.(1)求椭圆E的方程;
(2)求以点P(2,1)为中点的弦AB所在的直线方程.
分析 (1)由题意设出椭圆的标准方程,并求得c,再由离心率求得a,结合隐含条件求得b,则椭圆方程可求;
(2)设出A、B的坐标,代入椭圆方程,作差求得AB所在直线的斜率,代入直线方程的点斜式得答案.
解答 解:(1)设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由题意c=2,又$e=\frac{c}{a}=\frac{1}{2}$,得a=4,
∴b2=a2-c2=12.
∴椭圆E的标准方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)设A(x1,y1),B(x2,y2)代入椭圆E的方程得:
$\frac{{{x}_{1}}^{2}}{16}+\frac{{{y}_{1}}^{2}}{12}=1$ ①,$\frac{{{x}_{2}}^{2}}{16}+\frac{{{y}_{2}}^{2}}{12}=1$ ②,
①-②得:$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{16}=-\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{12}$,
∵点P(2,1)为AB的中点,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{12({x}_{1}+{x}_{2})}{16({y}_{1}+{y}_{2})}=-\frac{12×4}{16×2}=-\frac{3}{2}$.
即${k_{AB}}=-\frac{3}{2}$.
∴点P(2,1)为中点的弦AB所在直线的方程为y-1=$-\frac{3}{2}$(x-2),
化为一般式方程:3x+2y-8=0.
点评 本题考查椭圆标准方程的求法,考查椭圆的简单性质,训练了直线与椭圆位置关系的应用,属中档题.

| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充要也不必要 |
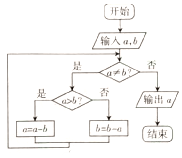 秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( )
秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( )