题目内容
20．已知函数$f（x）=\left\{\begin{array}{l}{log_3}x，x＞0\\ f（{x+2}），x≤0\end{array}\right.$，则$f（{f（{\frac{1}{9}}）}）$=log32．分析 由分段函数，运用对数的运算性质先求f（$\frac{1}{9}$），再由分段函数的第二段转化为f（2），即可得到所求值．
解答 解：函数$f（x）=\left\{\begin{array}{l}{log_3}x，x＞0\\ f（{x+2}），x≤0\end{array}\right.$，
可得f（$\frac{1}{9}$）=log3$\frac{1}{9}$=-2，
则$f（{f（{\frac{1}{9}}）}）$=f（-2）=f（0）=f（2）=log32．
故答案为：log32．
点评 本题考查分段函数的运用：求函数值，注意运用对应思想和转化法，考查运算能力，属于基础题．
练习册系列答案
特高级教师点拨系列答案
相关题目
10．
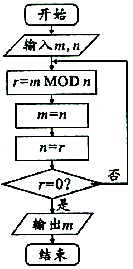如图所示，程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMODn”表示m除以n的余数），若输入的m，n分别为2016，612，则输出的m=（ ）
如图所示，程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMODn”表示m除以n的余数），若输入的m，n分别为2016，612，则输出的m=（ ）| A． | 0 | B． | 36 | C． | 72 | D． | 180 |
8．某电视台曾在某时间段连续播放5个不同的商业广告，现在要在该时间段只保留其中的2个商业广告，新增播一个商业广告与两个不同的公益宣传广告，且要求两个公益宣传广告既不能连续播放也不能在首尾播放，则不同的播放顺序共有（ ）
| A． | 60种 | B． | 120种 | C． | 144种 | D． | 300种 |
15．已知m，n是两条不同的直线，α，β是两个不重合的平面．命题p：若α∩β=m，m⊥n，则n⊥α；命题q：若m∥α，m?β，α∩β=n，则m∥n．那么下列命题中的真命题是（ ）
| A． | p∧q | B． | p∨￢q | C． | ￢p∧q | D． | ￢p∧￢q |
5．箱中装有标号为1，2，3，4，5，6且大小相同的6个球，从箱中一次摸出两个球，记下号码并放回，如果两球号码之积是4的倍数，则获奖，现有4人参与摸奖，恰好有3人获奖的概率是（ ）
| A． | $\frac{16}{625}$ | B． | $\frac{96}{625}$ | C． | $\frac{624}{625}$ | D． | $\frac{4}{625}$ |
2．若直线l过三角形ABC内心（三角形内心为三角形内切圆的圆心），则“直线l平分三角形ABC周长”是“直线l平分三角形ABC面积”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充要也不必要 |