题目内容
8．已知抛物线C：y2=2px（p＞0）的焦点为F，P是C上一点，过P点作C的切线l交x轴于Q点，且Q在C的准线上，则△PFQ一定是（ ）| A． | 等边三角形 | B． | 等腰直角三角形 | ||
| C． | 直角三角形但不是等腰三角形 | D． | 等腰三角形但不是直角三角形 |
分析 设P（$\frac{{m}^{2}}{2p}，m$），过点P的切线方程为：my=p（x+$\frac{{m}^{2}}{2p}$），
点Q（-$\frac{P}{2}$，0）在my=p（x+$\frac{{m}^{2}}{2p}$）上，0=（-$\frac{p}{2}$+$\frac{{m}^{2}}{2p}$）⇒m=p即可判定△PFQ的形状．．
解答 解：设P（$\frac{{m}^{2}}{2p}，m$），过点P的切线方程为：my=p（x+$\frac{{m}^{2}}{2p}$），
点Q（-$\frac{P}{2}$，0）在my=p（x+$\frac{{m}^{2}}{2p}$）上，0=（-$\frac{p}{2}$+$\frac{{m}^{2}}{2p}$）⇒m=p
∴P（$\frac{p}{2}$，p）．
故PF⊥x轴，且QF=PF=p，则△PFQ一定是等腰直角三角形，
故选：B．
点评 本题考查抛物线的切线方程及抛物线的性质，属于基础题，
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
5．箱中装有标号为1，2，3，4，5，6且大小相同的6个球，从箱中一次摸出两个球，记下号码并放回，如果两球号码之积是4的倍数，则获奖，现有4人参与摸奖，恰好有3人获奖的概率是（ ）
| A． | $\frac{16}{625}$ | B． | $\frac{96}{625}$ | C． | $\frac{624}{625}$ | D． | $\frac{4}{625}$ |
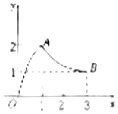如图，函数f（x）的图象是曲线OAB，其中点O，A，B的坐标分别为（0，0），（1，2），（3，1），则$f[{\frac{1}{f（3）}}]$的值等于2．