题目内容
函数f(x)是定义在实数集R上的不恒为零的偶函数,f(-1)=0,且对任意实数x都有xf(x+1)=(1+x)f(x),则f(0)+f(
)+f(1)+…+f(
)的值是 .
| 1 |
| 2 |
| 2011 |
| 2 |
考点:抽象函数及其应用,函数的值
专题:函数的性质及应用
分析:从xf(x+1)=(1+x)f(x)结构来看,要用递推的方法,先用赋值法求得,再由依此求解.
解答:
解:∵对任意实数x都有xf(x+1)=(1+x)f(x),
当x=0时,f(0)=0,
当x≠0时,f(x+1)=
f(x)
∴令x=-
,即f(
)=-f(-
),
又∵函数f(x)是定义在实数集R上的不恒为零的偶函数,
∴f(-
)=f(
),
∴f(
)=0,
令x=
,则f(
)=
f(
)=0,所以可得f(
)=f(
)=…=f(
)=0,
∵f(1)=f(-1)=0,
∵f(x+1)=
f(x)
∴f(1)=f(2)=f(3)=…=f(1005)=0,
所以f(0)+f(
)+f(1)+…+f(
)=0,
故答案为:0.
当x=0时,f(0)=0,
当x≠0时,f(x+1)=
| x+1 |
| x |
∴令x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵函数f(x)是定义在实数集R上的不恒为零的偶函数,
∴f(-
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
令x=
| 1 |
| 2 |
| 3 |
| 2 |
| ||
|
| 1 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 2011 |
| 2 |
∵f(1)=f(-1)=0,
∵f(x+1)=
| x+1 |
| x |
∴f(1)=f(2)=f(3)=…=f(1005)=0,
所以f(0)+f(
| 1 |
| 2 |
| 2011 |
| 2 |
故答案为:0.
点评:本题主要考查利用函数的主条件用递推的方法求函数值,这类问题关键是将条件和结论有机地结合起来,作适当变形,把握递推的规律.

练习册系列答案
相关题目
设a∈R,若函数y=ex+3ax(x∈R)有小于零的极值点,则( )
| A、-3<a<0 | ||
B、-
| ||
| C、a<-3 | ||
D、a<-
|
f(x)的定义域为R,f(2+x)=f(2-x),-1<x<2时,f(x)=(
)x,则有( )
| 1 |
| 2 |
A、f(-
| ||
B、f(4)<f(1)<f(-
| ||
C、f(1)<f(-
| ||
D、f(1)<f(4)<f(-
|
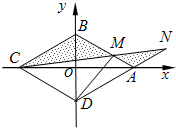 如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).