题目内容
函数f（x）=ax-1（a＞0，a≠1）的图象必过定点 ．
考点：指数函数的单调性与特殊点
专题：函数的性质及应用
分析：由指数函数的定义可知，当指数为0时，指数式的值为1，故令指数x-1=0，解得x=1，y=1，故得定点（1，1）．
解答：
解：令x-1=0，解得x=1，
此时y=a0=1，故得（1，1）
此点与底数a的取值无关，
故函数y=ax-1的图象必经过定点（1，1）
故答案为（1，1）．
此时y=a0=1，故得（1，1）
此点与底数a的取值无关，
故函数y=ax-1的图象必经过定点（1，1）
故答案为（1，1）．
点评：本题考点是指数型函数，考查指数型函数过定点的问题．解决此类题通常是令指数为0取得定点的坐标．属于指数函数性质考查题．
练习册系列答案
科学实验活动册系列答案
相关题目
下列给出的赋值语句中正确的是（ ）
| A、4=M | B、M=-M |
| C、B=A-3 | D、x+y=0 |
已知sinx+siny=
，则u=sinx+cos2x的最小值是（ ）
| 1 |
| 3 |
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|
方程x2-px+6=0的解集为M，方程x2+6x-q=0的解集为N，且M∩N={2}，那么p+q=（ ）
| A、21 | B、8 | C、6 | D、7 |
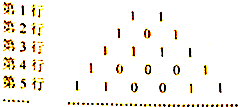将二项式系数表中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表，从上往下数，第1次全行的数都为1的是第1行，第二次全行的数都为1的是第3行，…，那么第61行中1的个数是